Table of Contents
신경망 학습
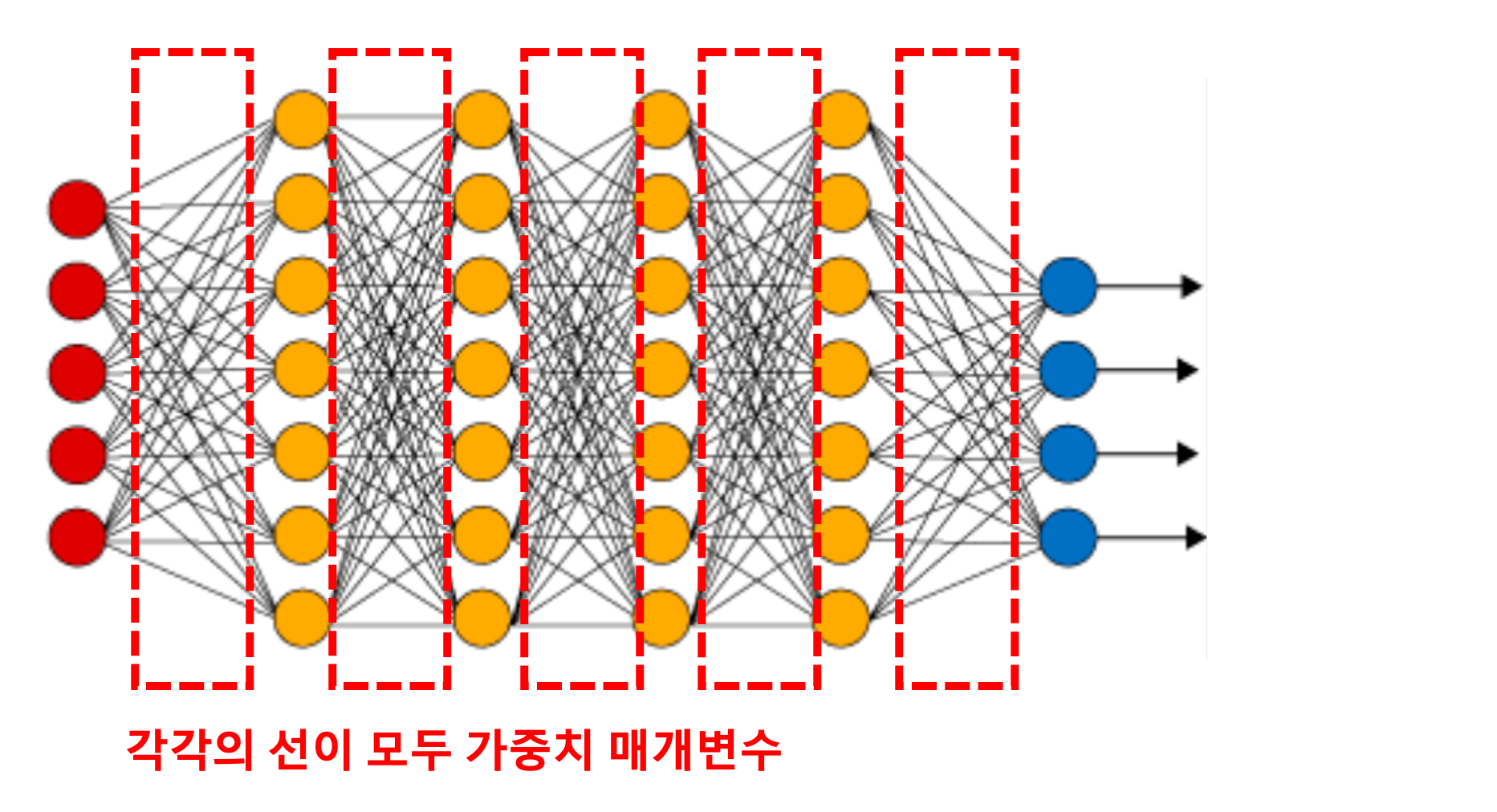
- 앞에서 살펴본 인공 신경망은 여러 층의 은닉층을 포함하고 있었다
- 각각의 은닉층에는 가중치라는 매개변수가 있다
- 학습이란 훈련 데이터로부터 가중치 매개변수의 최적값을 찾아내는 것을 말한다
- 가중치 매개변수의 최적값은 신경망 모델의 출력이 실제 값에 최대한 가까워질 때의 값을 의미한다
손실 함수
- 손실 함수는 신경망 모델의 출력과 실제 값의 차이를 수학적으로 정의한 함수를 의미한다
- 모델의 출력과 실제 값이 가까워지려면 두 값의 차이가 최소가 되어야 하므로, 우리는 손실 함수가 최소값이 되도록 학습을 하면 되는 것이다
- 손실 함수의 종류는 대표적으로 평균 제곱 오차(mean squared error, MSE)와 크로스 엔트로피 오차(cross entropy error)가 있다
MSE
- Mean Squared Error
- 회귀 문제에서 대표적으로 많이 사용되는 손실 함수이다
- (크로스 엔트로피 오차는 분류 문제에서 대표적으로 사용된다. 크로스 엔트로피는 나중에 분류 문제를 다루는 글에서 따로 다루도록 하겠다)
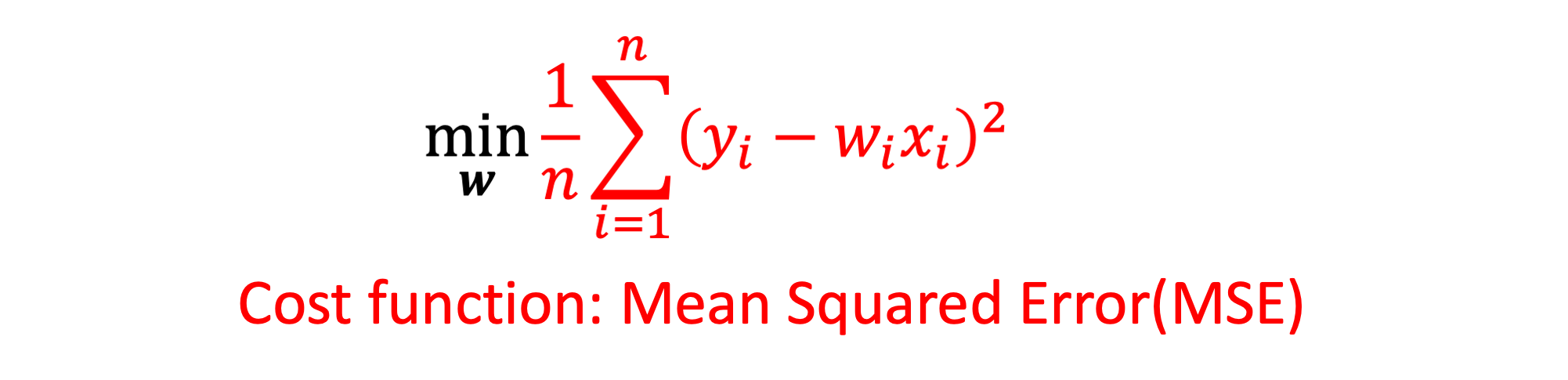
- 데이터 (
x(입력),y(정답레이블)) 쌍이 총100개 있다고 해보자 - 입력 데이터
1개마다 신경말 모델의 출력y_hat이 있고 이 값이 정답 레이블y1개와의 차이가 있다 - 하지만 입력 데이터
1개에만 잘 맞는 모델이 아니라, 데이터100개에 대해 평균적으로 잘 맞는 모델의 가중치를 찾아야 한다 - 그래서 전체 데이터 개수만큼 발생한 오차의 평균을 구해야 한다
- 또한 첫 번째 쌍에서 오차가
-2이고, 두 번째 쌍에서 오차가+2였다면 둘을 더하면0이 되어서 오차가 상쇄되는 문제가 생긴다 - 그래서 단순히 오차가 아니라, 제곱 오차를 구해야 한다
- (절대값이 아니라 제곱을 하는 이유는 제곱이 미분이 가능하기 때문이다. 미분이 되는 것이 나중에 배울 경사 하강법에서 이점이 있다)
가중치 업데이트
- 학습은 최적의 가중치 매개변수를 찾아내는 것이다
- 그러려면 학습 데이터(
(x, y))를 통과시킬 때마다 구해지는 오차를 최소화시키도록 가중치(w)를 업데이트 해야한다 - 은닉층에 있는 수많은 가중치들을 각각 어느정도 더하고 빼야 할까?
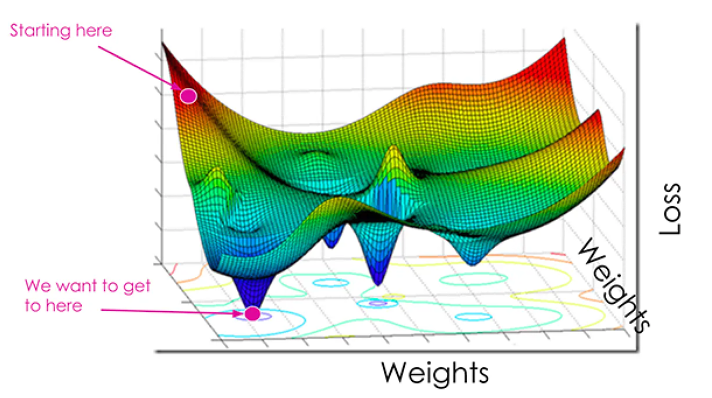
- 딥러닝에서는 이를 위해 경사 하강법(Gradient descent) 방법을 사용한다
- 그래디언트는 함수값을 가장 빠르게 증가시키는 방향이기 때문에 마이너스(-)를 취해주면 가장 빠르게 감소시키는 방향을 가르킨다
-
그래서 각 가중치 값마다 손실 함수의 미분을 구한 후, 상수값을 곱해서 이를 원래의 가중치에서 빼주면, 가중치는 점점 최적의 가중치에 가까워진다
- 가중치가 하나만 있다고 생각하고 경사 하강법을 시각적으로 단순화 시켜보면 아래와 같다
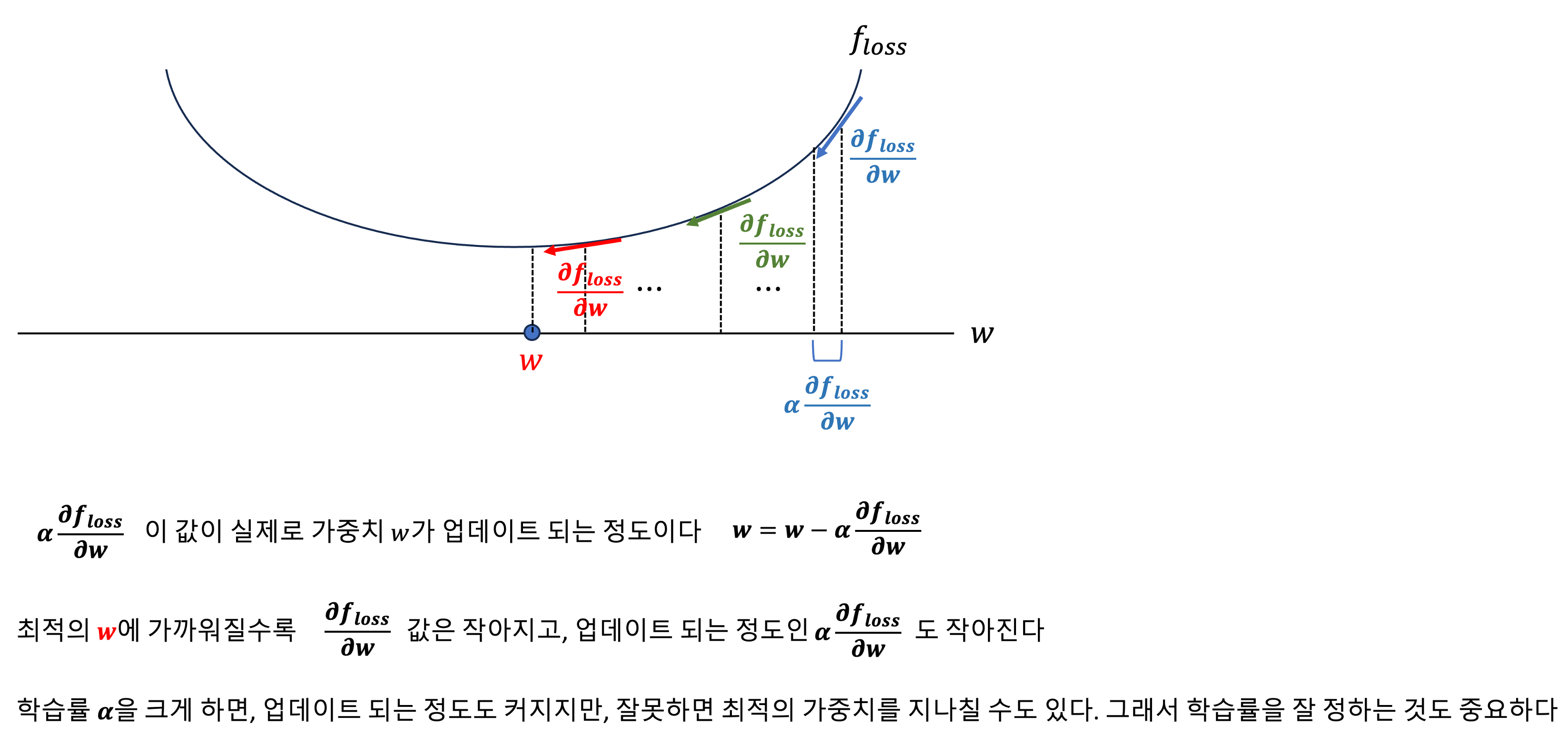
- 따라서 가중치가 여러개인 일반적인 상황에서는 손실 함수를 각 가중치에 대해 편미분하여, 각각의 가중치에 대해 업데이트 해주면 된다
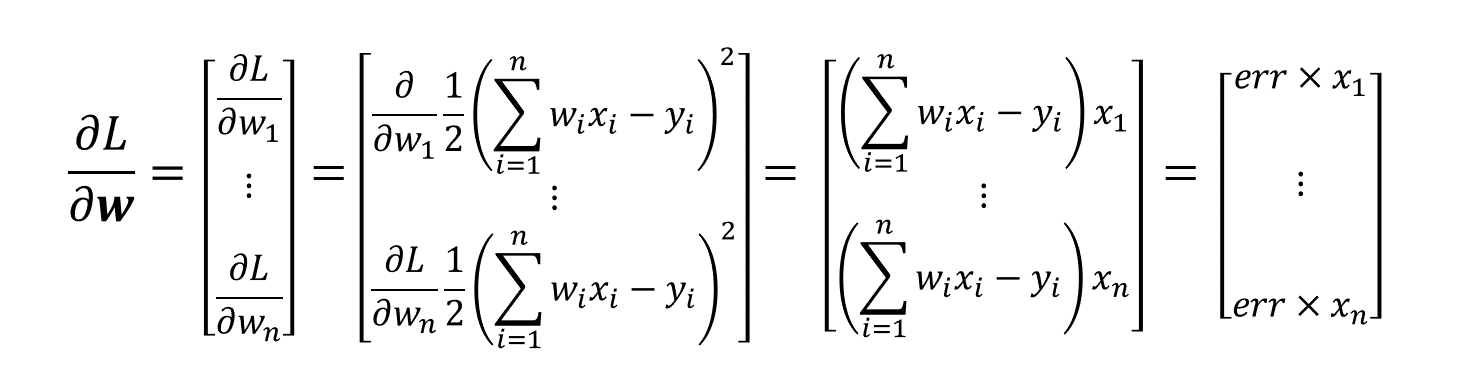
- 놀라운 사실은 MSE 함수의 미분 값은 결국 모델의 출력과 정답과의 차이인 오차(error)와 입력값(x)의 곱과 같다는 사실이다
- 마지막으로 이를 행렬로 나타내면 아래와 같다
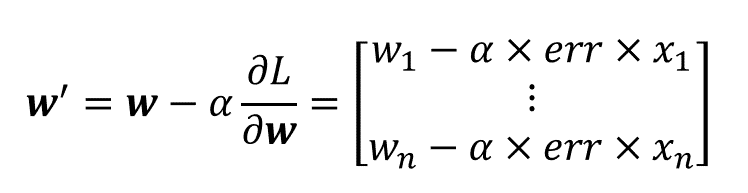



































![[AI Basic] 인공 신경망 학습](/images/ai_basic_logo.png)
