Table of Contents
추측 통계
- 모집단 전체를 모두 조사하는 방법을 전수조사(complete survey)라고 한다
- 전체에서 일부를 추출해 얻은 정보를 바탕으로 전체를 추측하는 방법을 표본조사(sample survey)라고 한다
- 모집단에서 일부를 추출할 때 비복원 추출이기 때문에 엄밀하게는 독립적인 시행이라고 할 수 없지만,
-
모집단의 크기가 표본의 크기와 비교해 충분히 큰 경우에는 복원 추출이라고 가정하며 결과적으로 추출을 독립 시행으로 바라본다
- 표본조사를 기반으로 하는 추측 통계 방법은 크게 추정(estimation)과 검정(test)으로 나뉜다
- 추정(Estimation): 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
- 점추정(point estimation): 표본 조사 결과를 가지고 모집단의 평균과 분산과 같은 값을 한 값으로 추정하는 경우
- 구간추정(interval estimation): 평균과 분산과 같은 값의 폭을 추정하는 경우
- 검정(Testing): 표본을 토대로 모집단에 관한 가설을 세우고 옳고 그름을 판별하는 과정
- 추정(Estimation): 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
검정
- 어떤 가설이 옳은지를 통계적으로 판단하는 가설검정(hypothesis testing)
- 데이터 분석에서 분석한 결과를 통계적으로 뒷받침 하는 근거가 된다
- 가설검정에서는 우선 검정하고자 하는 가설을 우연히 발생한 일로 가정하고, 이를 기각하는 방식으로 검정한다
- 이때 기각하고자 하는 가설을 귀무가설(H0)이라 하고, 귀무가설을 기각함으로써 증명하고자 하는 가설을 대립가설(H1)이라 한다
- 그러면 가설검정에서는 어떤 기준으로 기각을 정할까? 보통 발생할 확률이 5% 이상이면 우연히 발생할 수 있는 일이라 생각한다
- 그래서 우연히 발생한 일로 가정하고 확률을 계산했을 때 5% 이하면, 우연히 발생하기 힘든 일이라 생각하고 귀무가설을 기각하고 대립가설을 채택한다
- 여기서 5%는 보통 많이 사용되는 유의수준이며, 더 엄격한 기준을 적용하고 싶으면 더 작은 값을 사용하면 된다
- 데이터를 EDA 하면서 아이디어가 떠오른다
- 아이디어를 검정할 수 있도록 가설을 세워본다
- 어떤 검정 통계량으로 증명할지 정한다 (평균, 분산, 비율 등)
- 검정 통계량이 따르는 분포가 무엇인지 알아낸다
- 최종적으로 검정 통계량의 p-value를 구해 가설을 검정한다
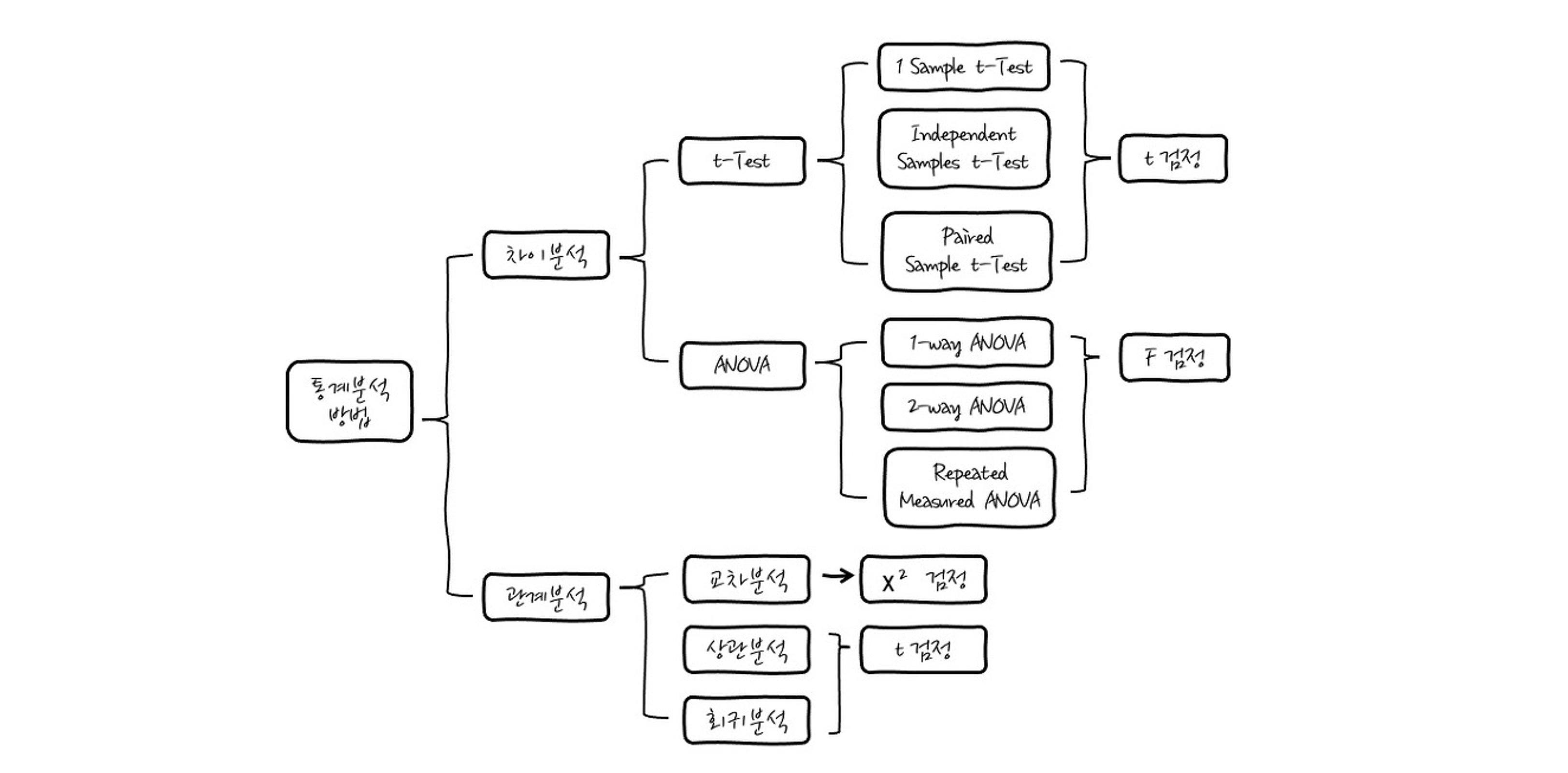
t 검정
- 표본평균이 따르는 분포로, 표본크기가 커질수록 정규분포에 가까워진다
- 모분산을 모를 때, 모분산 대신 표본분산을 이용하는 경우
- 보통 집단 간 차이를 볼 때는 대표값인 표본평균을 이용한다
- 두 집단의 차이는 두 집단의 표본평균의 차이로 차이검정을 하는데, 표본평균이 t분포를 따르기 때문에, 표본평균의 차도 여전히 t분포를 따른다
- 그래서 두 집단의 표본평균의 차이가 0인 경우를 귀무가설로 설정하여 검정한다
ex. 어떤 다이어트 보조 음료에 관한 설문조사를 했는데 100명중 62명이 효과가 있었다고 답했다. 이때 이 보조 음료는 다이어트 효과가 있다고 말할 수 있을까?
- 귀무가설: 62명이 효과있다고 말한 일은 그저 우연이다
- 대립가설: 우연이 아니다. 진짜 보조 음료가 효과가 있다
- 귀무가설이 일어날 확률이 보통 5% 이상이면, 우연이라 판단하고 귀무가설을 채택
- 귀무가설이 일어날 확률이 5% 이하면, 우연이라 보기 힘들기 때문에 대립가설을 채택
- 귀무가설이 발생할 확률: 효과 있다/없다 선택할 확률 1/2. 이를 100번 시행했을 때 62명이 있다고 할 확률
- 평균은 np 이므로 50, 표준편차는 np(1-p)이므로 25
- 표준화시키면 (62 - 50) / 5 = 2.4 => 정규분포표를 이용해 계산해보면 확률은 1.6%가 나온다
- 5% 이하이므로 매우 낮다 => 이렇게 낮은 확률의 일이 우연히 발생했을 리 없다 => 우연이 아니다 => 효과가 있다 (대립가설 채택)
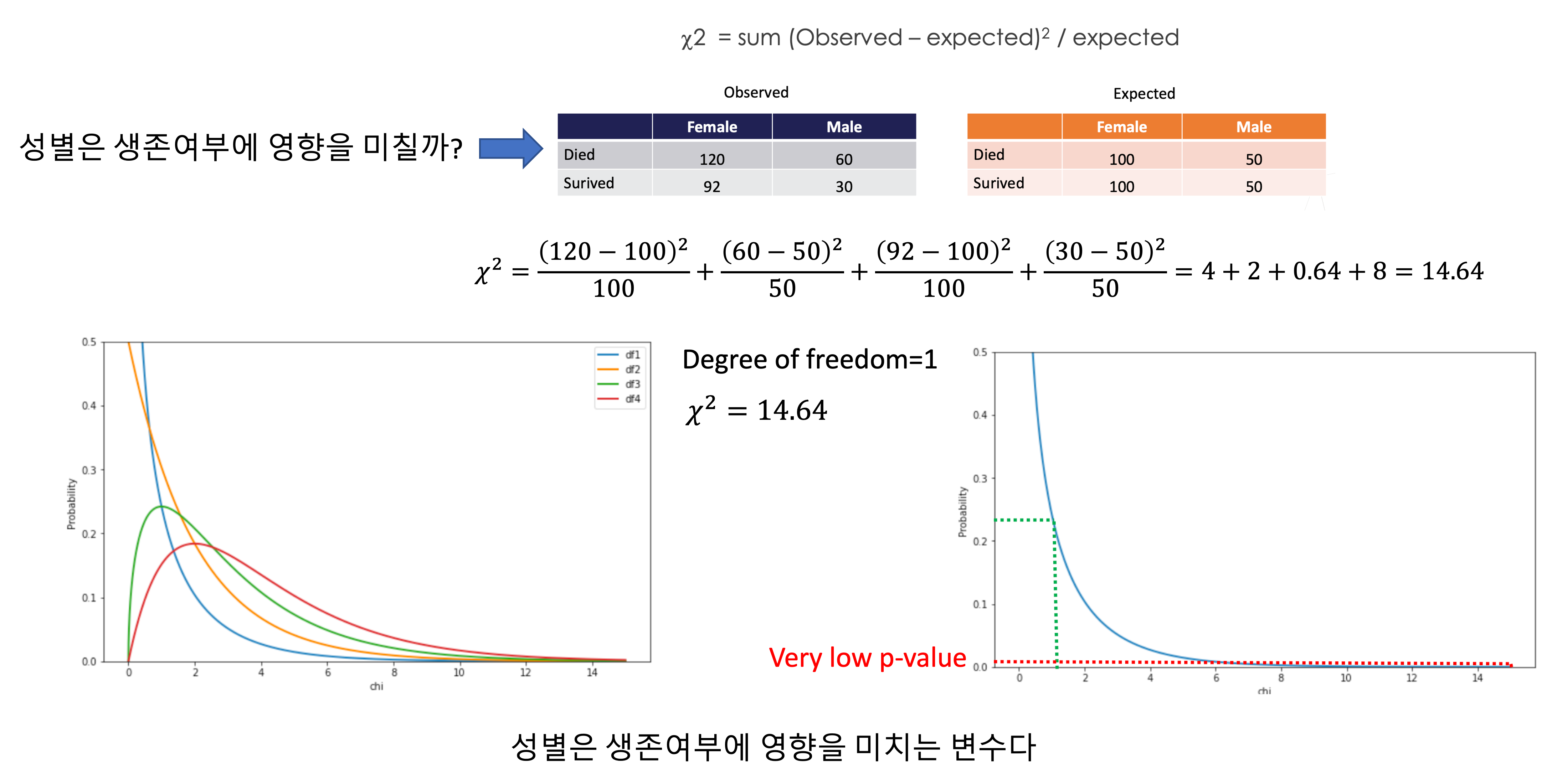
카이제곱 검정

- 가우시안을 따르는 확률변수의 제곱의 합은 카이제곱 분포를 따른다
- 두 범주형 변수가 서로 관련이 있는지 없는지 검정하는데 사용한다
- (독립적이면 서로 관련 없음. but 관련 없다고 해서 독립적이라고 할 순 없음)
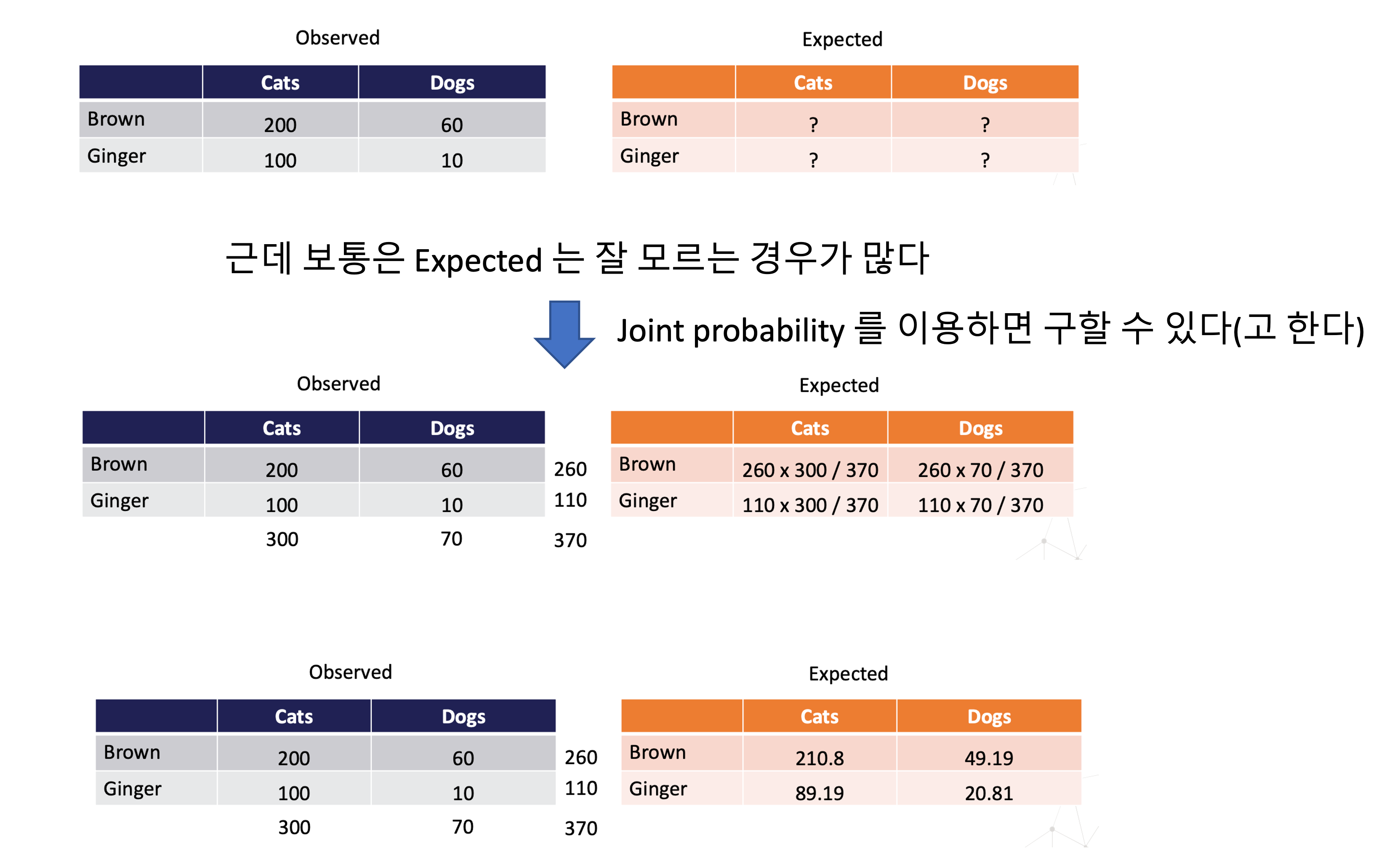
F 검정

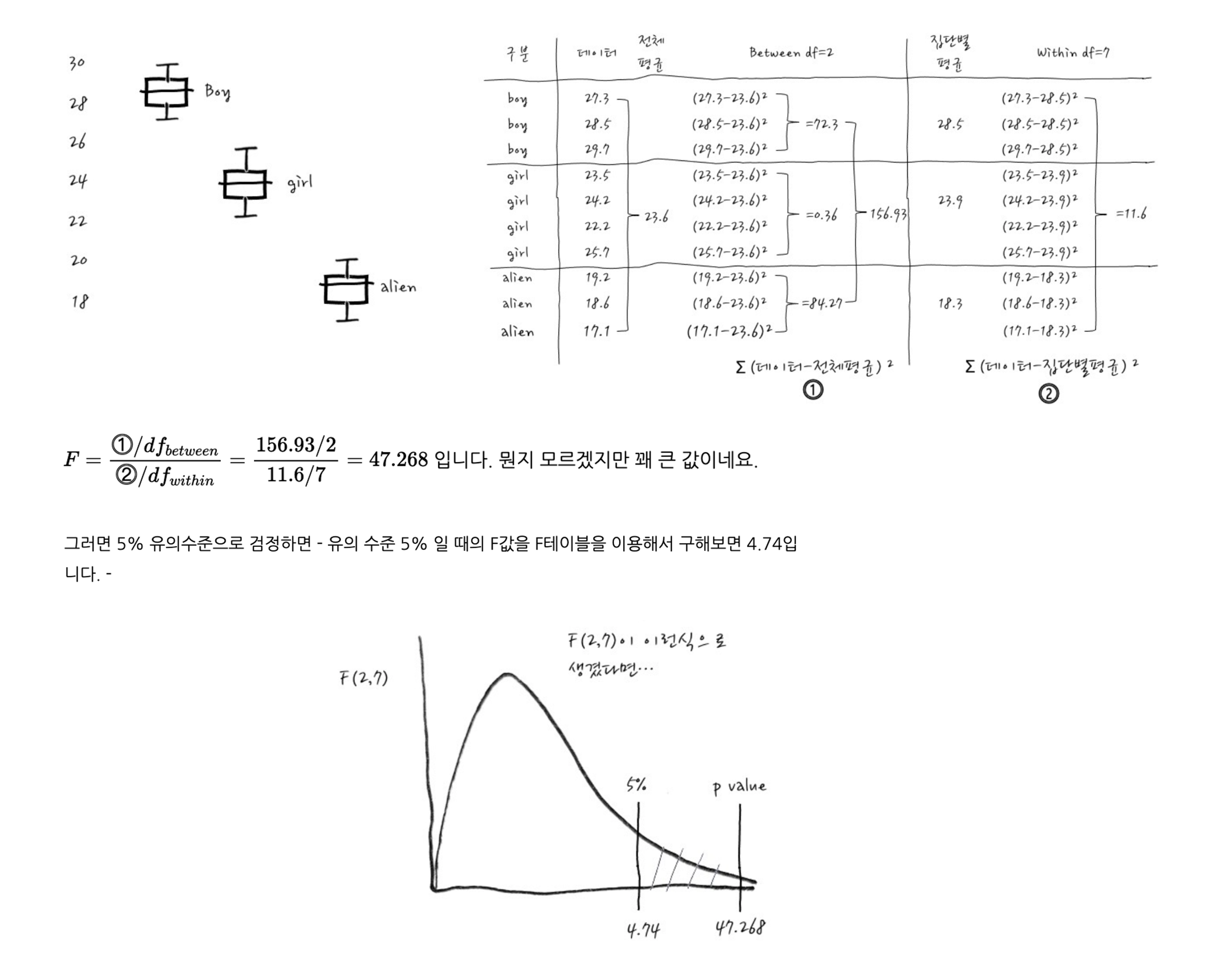
- 카이제곱 분포와 카이제곱 분포를 따르는 확률변수간의 비는 F분포를 따른다
- 대표적으로 분산과 분산의 비가 F 분포를 따른다
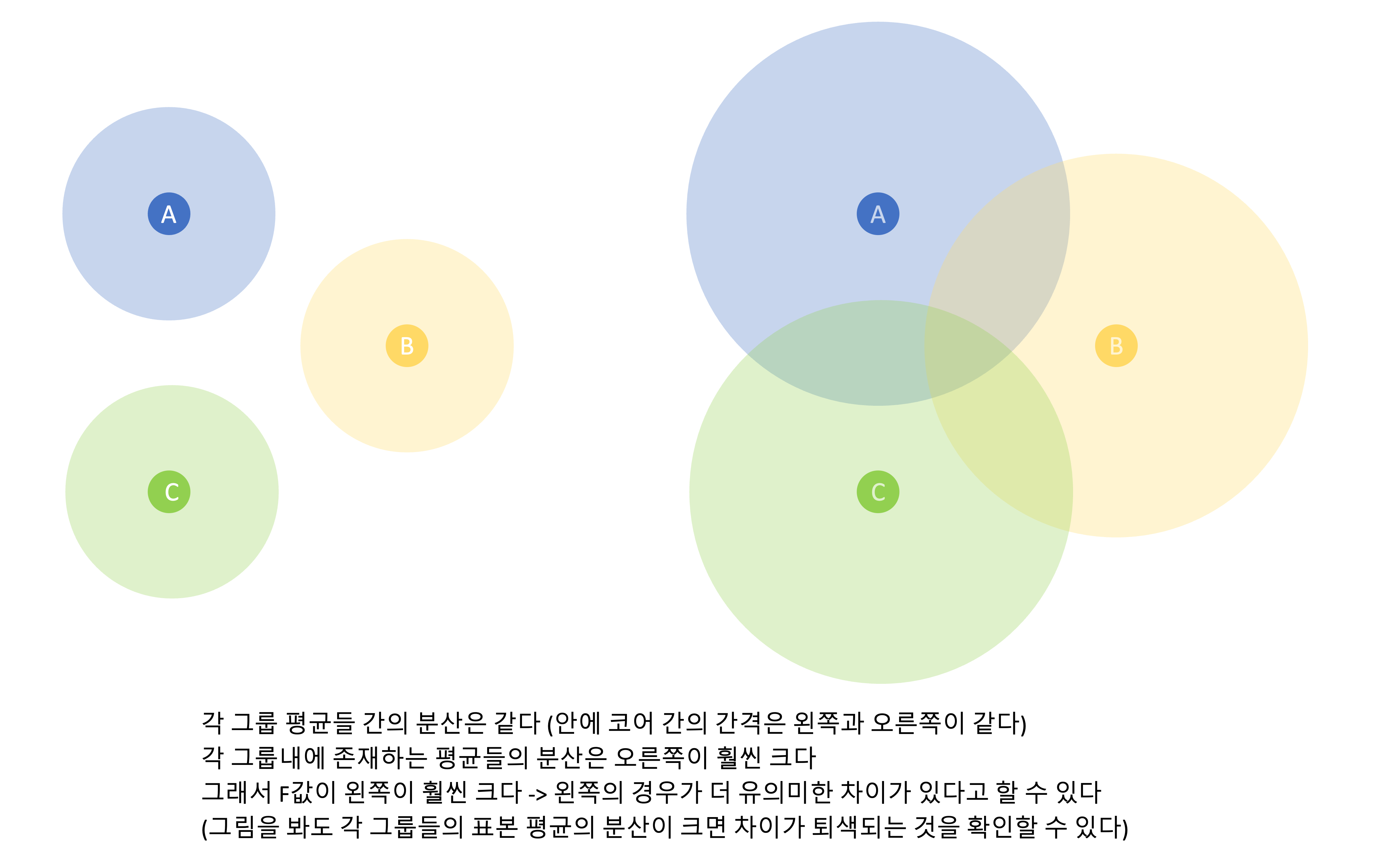
- F비는 ANOVA라는 분산분석에서 이용한다
- 세 개 이상의 집단 간의 유의미한 차이가 있는지 검정할 때 사용한다



































![Statistics and Probability Series [Part6]: 추측 통계(2): 검정(Testing)](/images/probability_logo.jpeg)
