Table of Contents
추측 통계
- 모집단 전체를 모두 조사하는 방법을 전수조사(complete survey)라고 한다
- 전체에서 일부를 추출해 얻은 정보를 바탕으로 전체를 추측하는 방법을 표본조사(sample survey)라고 한다
- 모집단에서 일부를 추출할 때 비복원 추출이기 때문에 엄밀하게는 독립적인 시행이라고 할 수 없지만,
-
모집단의 크기가 표본의 크기와 비교해 충분히 큰 경우에는 복원 추출이라고 가정하며 결과적으로 추출을 독립 시행으로 바라본다
- 표본조사를 기반으로 하는 추측 통계 방법은 크게 추정(estimation)과 검정(test)으로 나뉜다
- 추정: 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
- 점추정(point estimation): 표본 조사 결과를 가지고 모집단의 평균과 분산과 같은 값을 한 값으로 추정하는 경우
- 구간추정(interval estimation): 평균과 분산과 같은 값의 폭을 추정하는 경우
- 검정: 표본을 토대로 모집단에 관한 가설을 세우고 참, 거짓을 판별하는 방법
- 추정: 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
모집단과 표본
- 모집단의 어떤 변량에 관한 분포를 모집단 분포라하고, 모집단 분포를 특징짓는 상수를 모수(모평균, 모분산, 모표준편차 등)라고 한다
- 모집단에 관한 정보는 이미 확정되어 있다
- 표본집단은 일반적으로 매번 다르다. 그래서 E(X)도 일반적으로 매번 다르다
- E(X)는 ∑(Xk*pk) 이므로 E(X)도 확률변수가 될 수 있다
표본평균의 평균과 표준편차
- 표본평균의 평균, 분산 그리고 표준편차는 아래와 같다
- 표본 크기 n이 커질수록 표본평균의 표준편차가 작아진다
- (모집단에서 추출을 충분히 많이 하면, 표본의 평균이 표본집단마다 거의 같아진다는 의미이다)
- (m은 모평균, σ는 모표준편차)
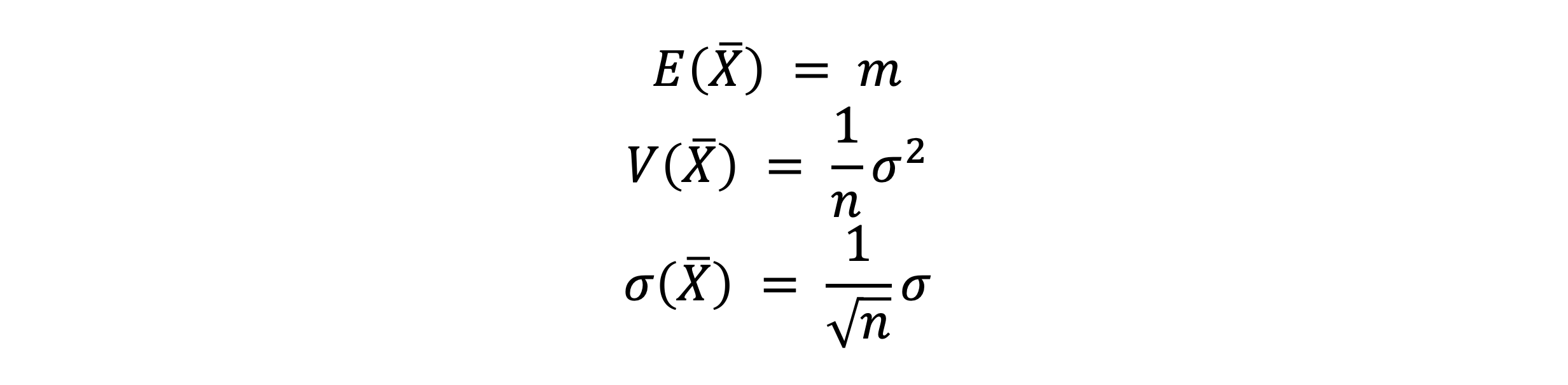
- 우리의 목표는 어디까지나 모집단을 예측하는 것이다
- 위의 식을 보면 표본평균의 평균과 표준편차는 모집단의 평균 표준편차와 밀접한 관계가 있음을 알 수 있다
- 그렇기 때문에 표본을 조사하는데 의미가 있고 추정이 가능한 것이다
큰수의 법칙
- 발생확률이 수학적으로 p인 사건을 반복 시행할 때, n이 작으면 경험적 확률과 수학적 확률간의 차이가 크다
- 하지만 반복시행의 크기 n이 커지면, 경험적 확률이 수학적 확률에 수렴하게 된다(한없이 가까워진다)
- 모집단에 빨간색이 700개, 파란색이 300개 있었다면, 표본의 크기가 커질수록 표본집단에도 빨간색이 70%, 파란색이 30% 비율로 있게 된다
- 큰 수의 법칙: 표본의 크기가 커질수록 표본평균 E(X)는 모평균 m에 가까워진다
- (표본의 크기가 크면 클수록 해당 표본에서 구한 평균이 실제 모평균일 가능성이 높아진다)
중심극한정리
- 모집단에서 n > 30 이상인 표본의 표본 평균은, 평균이 모평균이고 분산이 σ2/n 인 정규분포를 근사적으로 따른다
- 모집단이 어떤 분포라도 표본평균의 분포는 정규분포로 가까워진다
- 중심극한정리 덕분에 가능해진 것이 바로 추정이다
추정
점추정
- 점추정: 표본에서 구한 추정값으로부터 모수값을 추정하는 방법
- (즉, 표본 평균을 모평균으로, 표본 분산을 모분산으로 생각할 수 있을까?)
- 이에 대해 “예”라고 대답하기 위해서는 두 가지 조건을 만족해야 한다
- 비편향성: 기대값이 모수값과 같다
- (표본평균의 평균이 모평균과 같으면 표본평균을 모평균이라고 할 수 있다)
- (표본분산의 평균이 모분산과 같으면 표본분산을 모분산이라고 할 수 있다)
- 일치성: 표본의 크기가 커지면 모수값에 가까워진다
- 비편향성: 기대값이 모수값과 같다
- 위에서 표본평균의 평균은 m 이고, 분산은 σ<sup2</sup>/n 이라고 배웠으므로, 표본평균을 모평균이라고 할 수 있다
- 이제 표본분산의 평균이 σ2과 같은지 확인해보자. 계산하면 (n-1/n)σ2이 나온다
- 그래서 비편향성을 가지지 않는다. 그래서 n/n-1 을 곱해 보정한 값을 비편향 분산이라고 하고, 보통 모분산을 (n/n-1)*S2 으로 한다 (S2는 표본분산)
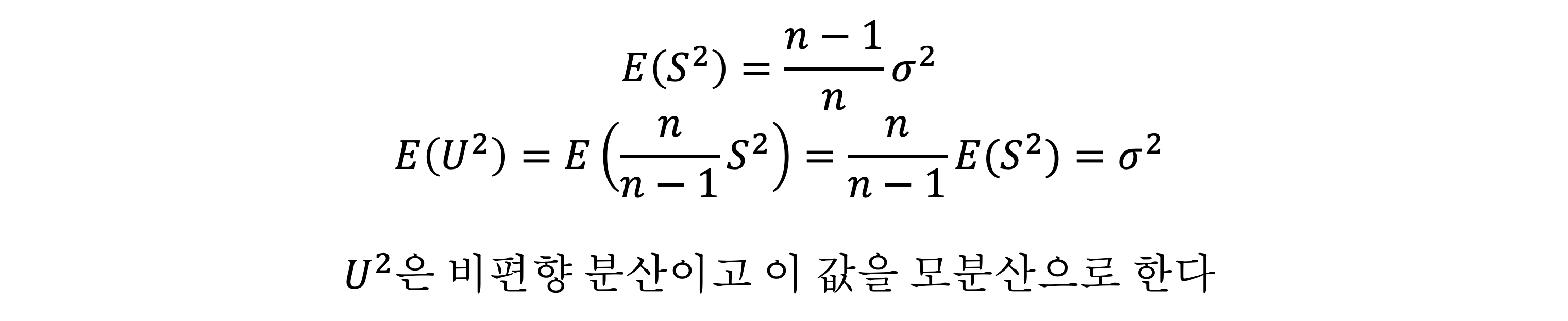
- 점추정은 값이 딱 나와서 명료하지만 표본의 크기에 의한 오차를 고려할 수 없어서 한계가 있다
구간추정
- 추정한 모수값이 특정 범위내에 있을거라고 (ex. 95, 99, 99.9)%의 신뢰도를 가지고 추정할 수 있다

- 근데 실제로 추정을 수행할 때는 모분산도 모르는 경우가 많다
- 결론은 표본의 크기가 100이하면 비편향 분산을, 100이상이면 표본분산을 쓰면 된다



































![Statistics and Probability Series [Part5]: 추측 통계(1): 추정(Estimation)](/images/probability_logo.jpeg)
