![Statistics and Probability Series [Part4]: 확률(2) 확률 분포](/images/probability_logo.jpeg){kind=logo}
Table of Contents
확률변수와 확률 분포
- 확률변수: 어떤 값이 되는지는 시행결과에 따라 정해지고, 발생할 확률이 정해져 있는 사건을 수치화 한 것
- ex. 주사위를 던졌을 때 나오는 수는 1/6 이라는 확률을 가지고, 각각을 1, 2, 3, 4, 5 ,6 이라는 숫자로 수치화 할 수 있다
- ex. 동전을 2번 던졌을 때 앞면의 수는 1/4, 1/2, 1/4 이라는 확률을 가지고, 각각을 0, 1, 2 라는 숫자로 수치화 할 수 있다
- 어떤 변수 X가 확률변수라는 말은 X에 대한 확률분포를 알고 있다는 말
- 수치화된 값이 띄엄띄엄 떨어져 있는 경우 이산확률 변수(discrete random variable)
- 값이 연속적인 경우 연속확률 변수
확률변수의 평균과 분산
확률변수의 평균
- 확률변수의 평균은 기대값(expectation)이라는 말을 많이 쓴다
- 왜냐하면 이미 발생한 사건에 대한 평균이 아닌, 관측할 때 나타날 것으로 기대되는 값을 뜻하기 때문이다
- (확률변수의 기대값은 과거 데이터를 가지고 계산한 것이 아니라, 앞으로 몇 번이고 같은 시행을 반복한다고 할 때 결과적으로 가까워지리라 기대되는 평균값)
- 확률변수의 기대값이 획기적인 이유: 실제로 관측하기 전에 평균값을 예측할 수 있다
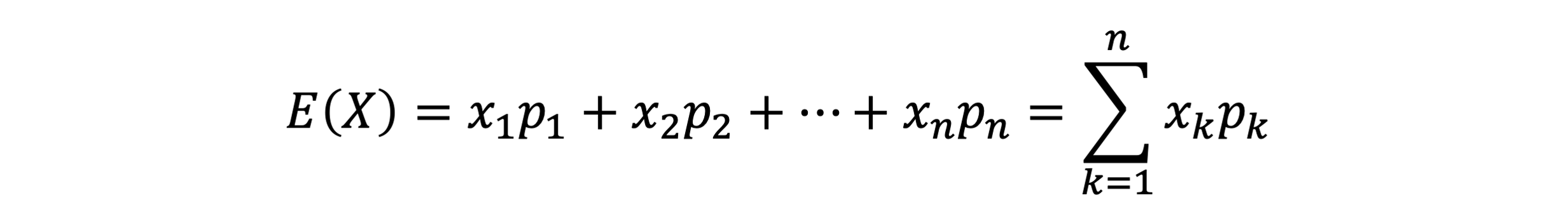
확률변수의 분산
- 확률변수에서도 X의 각 값과 m이 떨어진 정도를 제곱하여 평균을 구한 값을 분산이라고 한다
- 확률변수의 표준편차는 기대값에서부터 떨어진 값이 나올 가능성을 나타냅니다
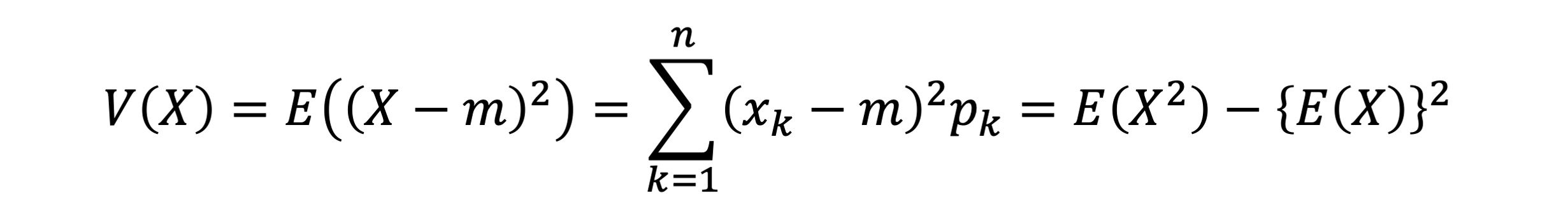
확률변수의 변환
- X가 확률변수 일 때 확률변수 Y=aX+b의 평균과 분산은 어떻게 될까
- X가 x1 값이 될 확률이 p1이면, Y가 y1 값이 될 확률도 p1 이다
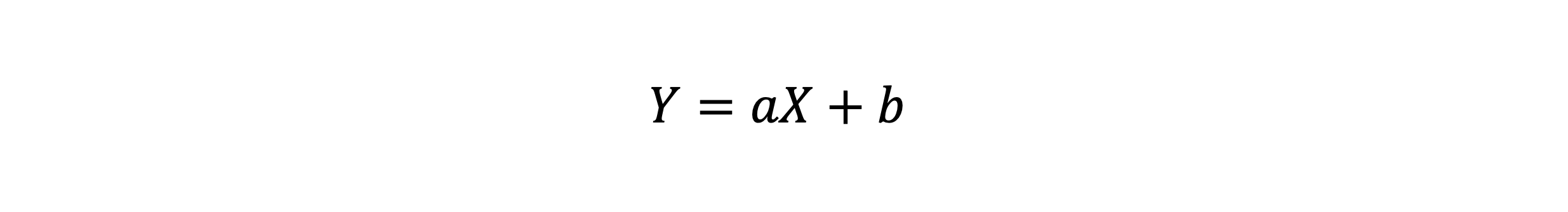
- 평균은 다음과 같다
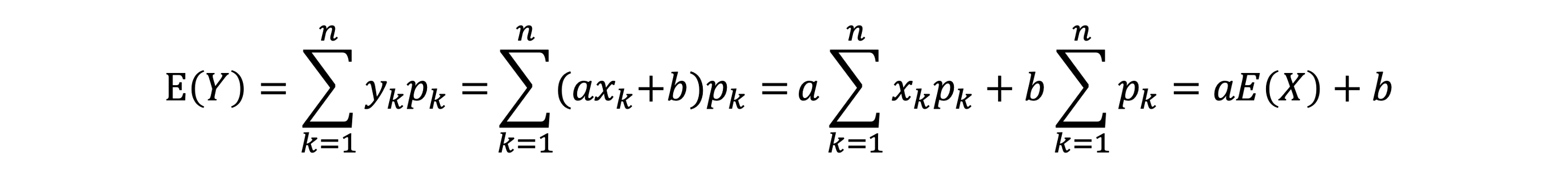
- 분산은 다음과 같다
- 모든 값에 b를 더하는 것은 흩어진 정도에는 영향을 주지 않는다
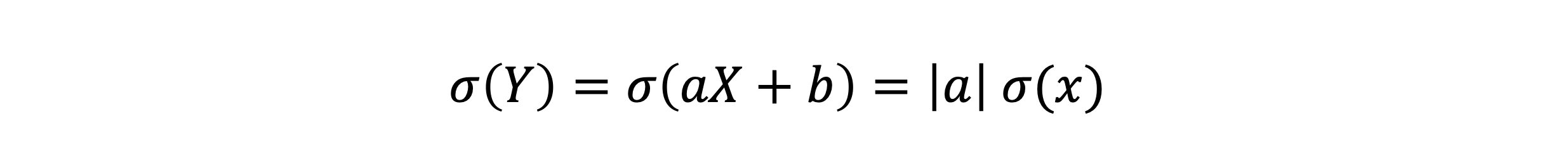
확률 변수의 표준화
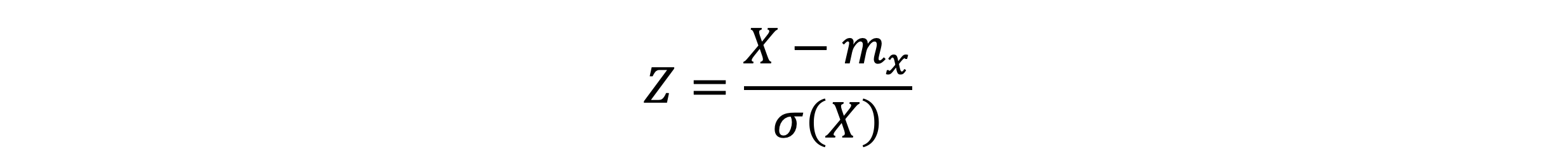
- 위의 식의 평균과 분산을 계산해보자
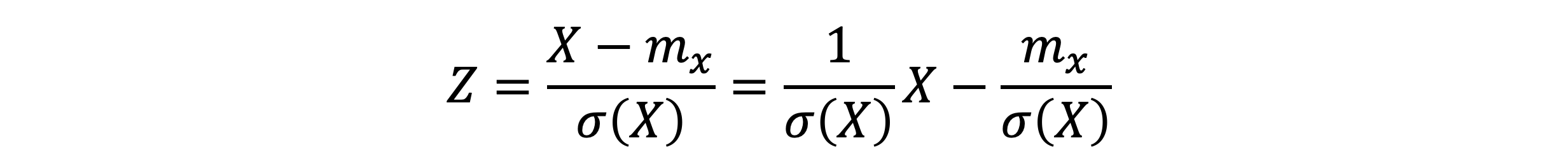
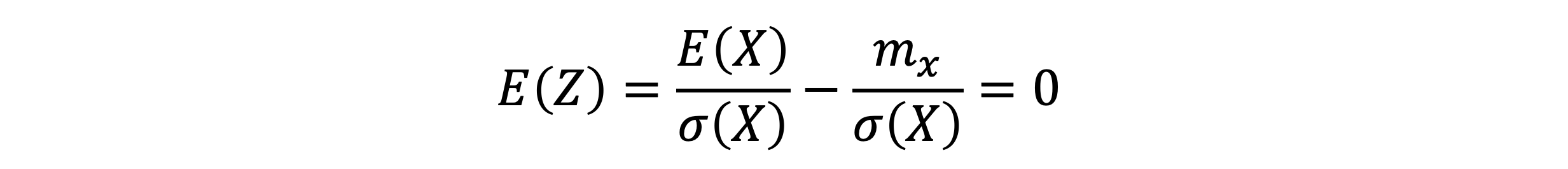
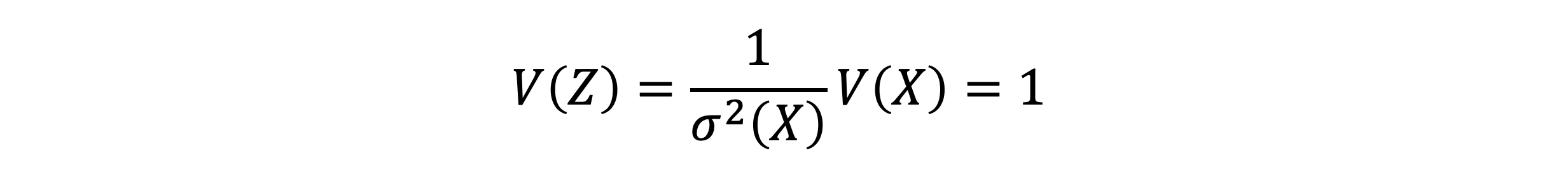
- 어떤 확률변수에서 평균을 빼고 표준편차로 나눈 확률변수 Z의 평균과 분산은 항상 0, 1이다
- 이 말은 평균이 0이고 표준편차가 1인 확률변수에 관해 여러 가지 성질을 알아두면, 다른 확률변수에 응용할 수 있다는 의미이다
확률변수의 합과 곱
- 확률변수 합의 예시: A가 던진 주사위의 숫자와 B가 던진 주사위의 숫자의 합에 대한 기대값, 표준편차
- 확률변수 곱의 예시: A가 던진 주사위의 숫자와 B가 던진 주사위의 숫자의 곱에 대한 기대값, 표준편차
확률변수의 합의 기대값
- 확률변수의 합의 기대값은 아래와 같다
- 이 식은 X와 Y가 서로 독립이 아닌 경우에도 성립한다
확률변수 합의 분산
- 확률변수 합의 분산은 X, Y가 서로 독립일 때 아래와 같다
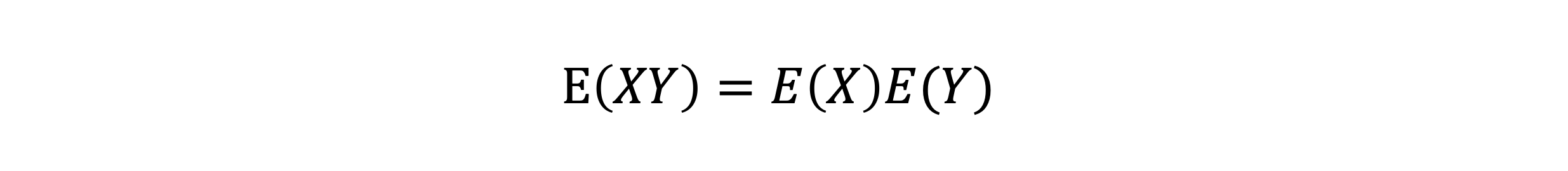
확률변수 곱의 기대값
- 확률변수 곱의 기대값은 X, Y가 서로 독립일 때 아래와 같다
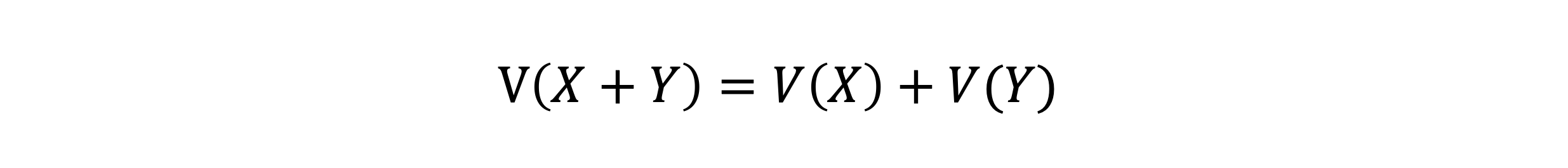
이산확률변수
이항분포
- 이항분포: 반복시행의 확률분포
- 1회 시행으로 사건 A가 일어날 확률이 p일 때, 이 시행을 n번 반복할 때 A가 k번 일어날 확률은 아래와 같다
- (이렇게 앞/뒤, 승/패 처럼 결과가 둘 중 하나가 되는 독립인 시행을 베르누이 시행이라고 한다)
- 베르누이 시행을 반복하는 반복시행의 확률분포가 이항분포이다
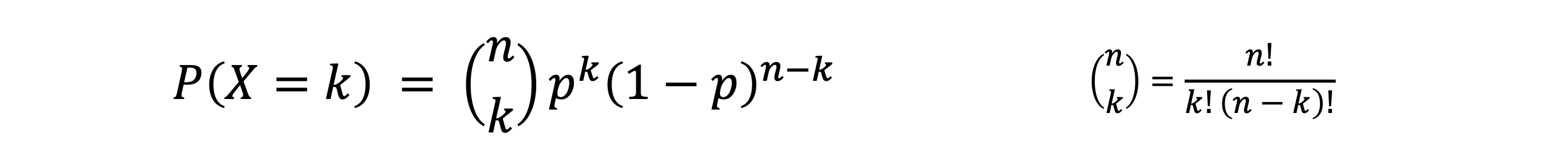
- 이항분포는 아래와 같다
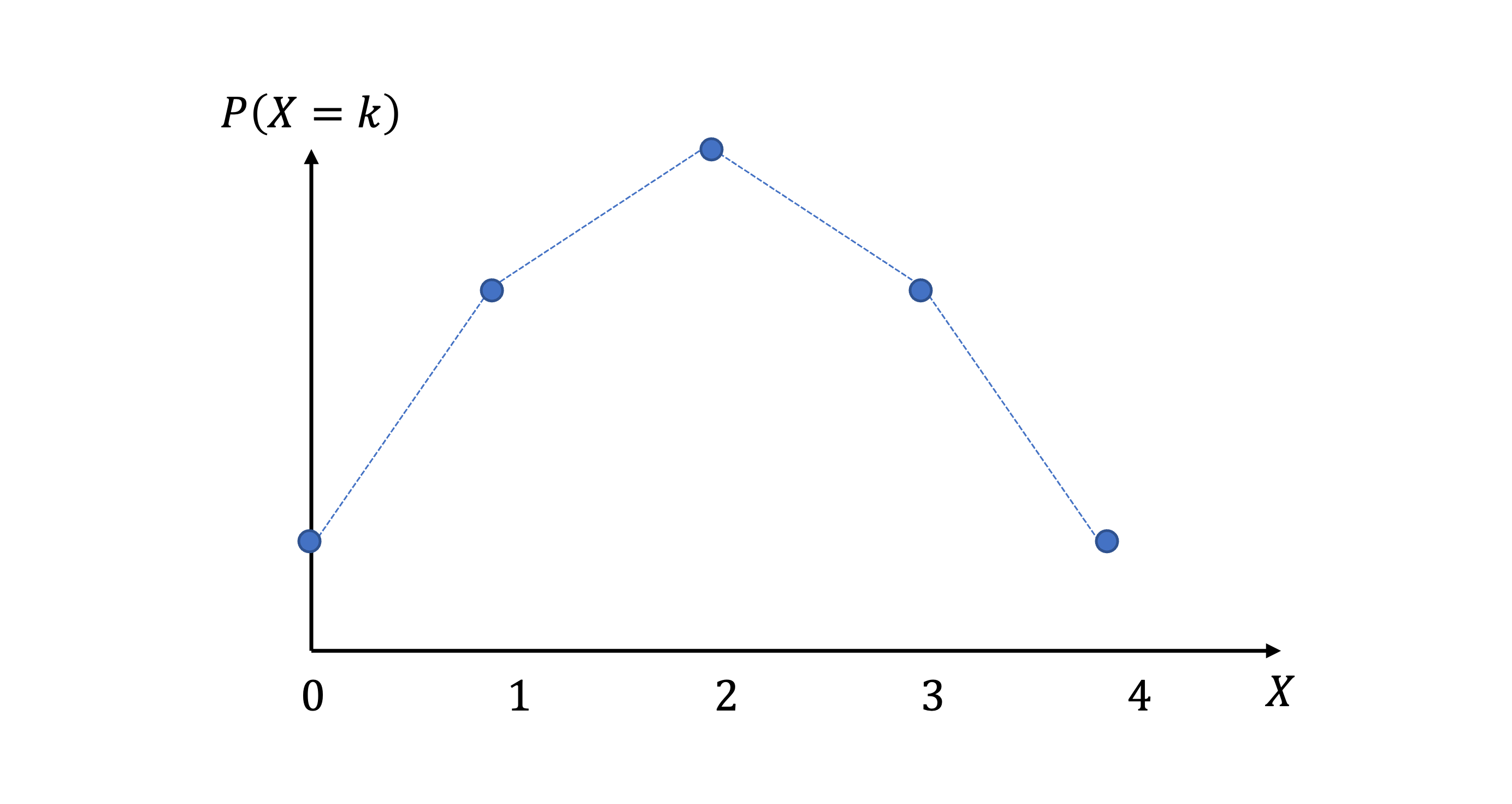
- 이항분포의 기대값, 분산, 표준편차는 아래와 같다
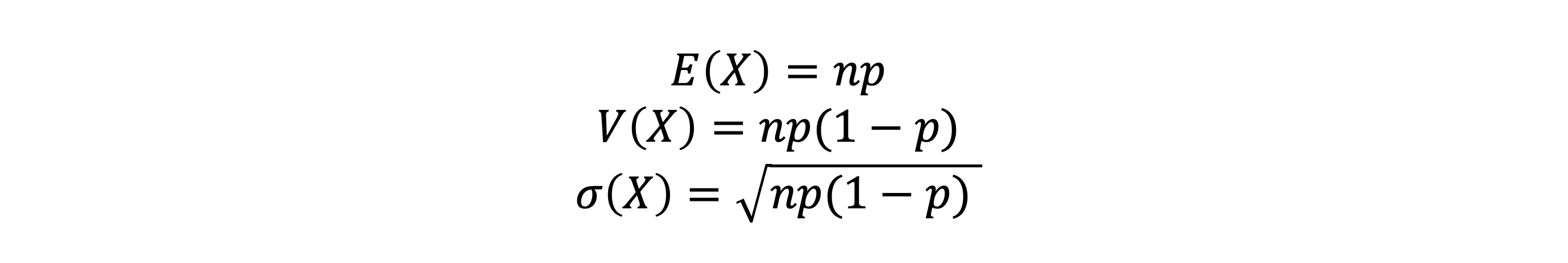
푸아송 분포
- 어떤 제품을 만들 때 불량률이 p=0.001 라고 해보자. 제품 1000개를 만들 때 불량품 2개가 발생할 확률은?
- 이 계산은 매우 귀찮다
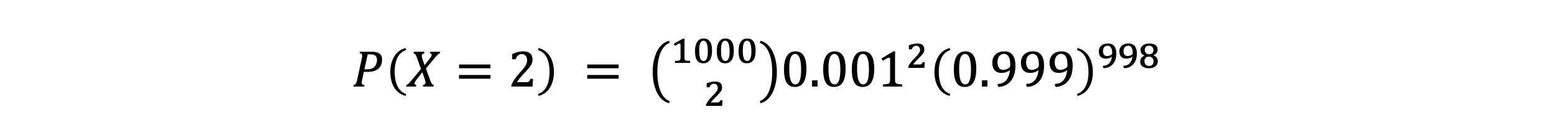
- n이 크고(100 이상), p가 낮을 때(0.01 이하), 이항분포의 좋은 근사가 되는 분포가 있다. 바로 푸아송 분포(Poisson distribution)다
- 푸아송 분포는 시행횟수가 매우 많으면서 발생할 확률이 매우 적은 반복시행의 확률분포와 매우 유사하다
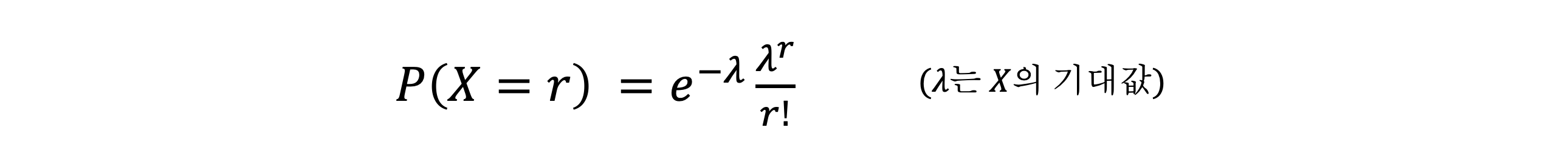
연속확률변수
- X가 될 수 있는 값이 연속적이다
- 더이상
특정 사건의 수 / 모든 사건의 수와 같은 방식으로 확률을 계산할 수 없다 (=> 정확히 키가 170cm 일 확률을 계산할 수 없다) - 이산확률변수에서 확률변수는 특정 사건의 확률이 정해져 있는 경우에 확률변수가 될 수 있었다
- 연속확률변수에서 확률변수는 특정 범위에 포함될 확률이 정해져 있으면 확률변수가 될 수 있다
- 연속확률변수에서 기대값, 분산, 표준편차는 아래와 같다
- 연속확률변수의 분포를 확률밀도함수(Probability Density Function)이라고 한다
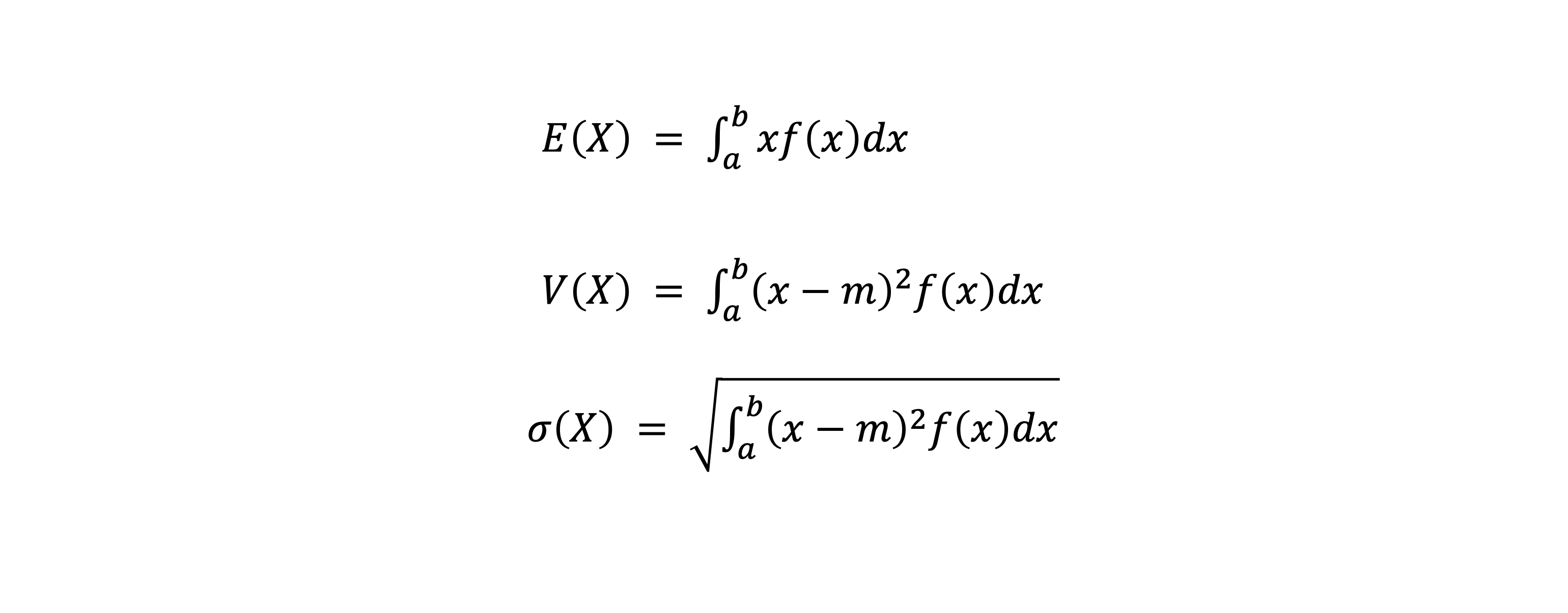
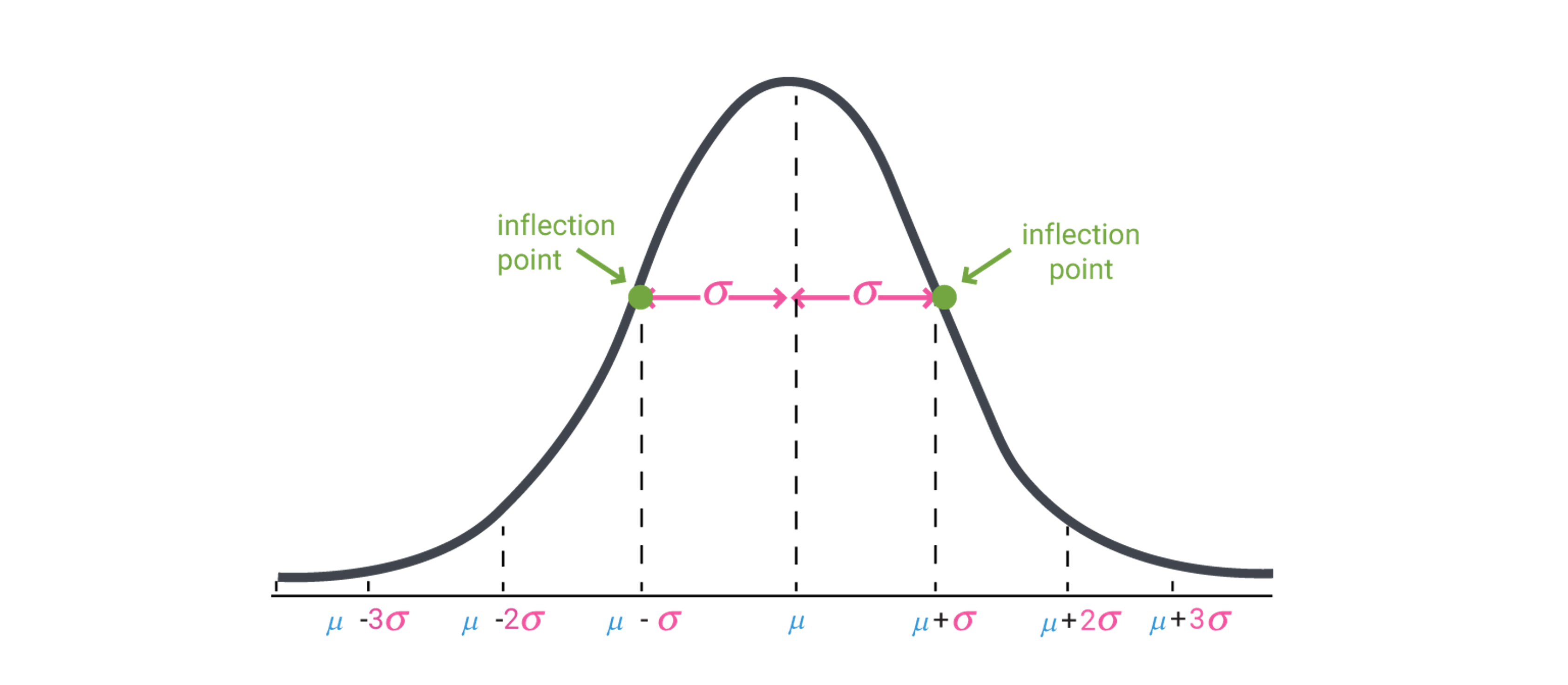
정규분포
- 가장 자주 등장하고 가장 중요한 확률밀도함수
- 실생활에서 발생되는 오차의 크기는 대부분 정규분포로 모델링 할 수 있다
- 이항분포를 정규분포로 근사할 수 있다
- 모집단에서 추출한 표본의 평균은 정규분포가 된다 (중심극한정리)
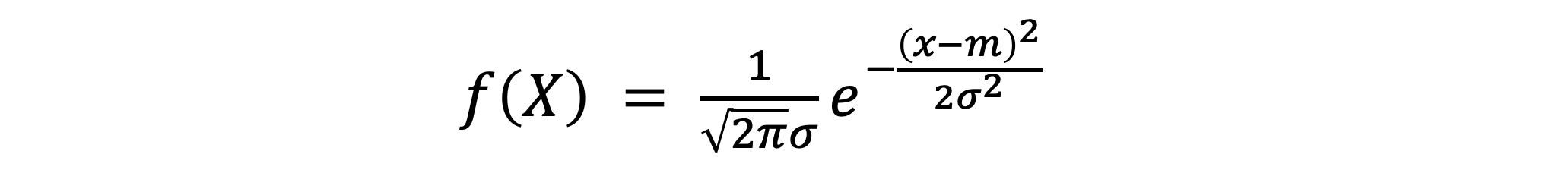
표준정규분포
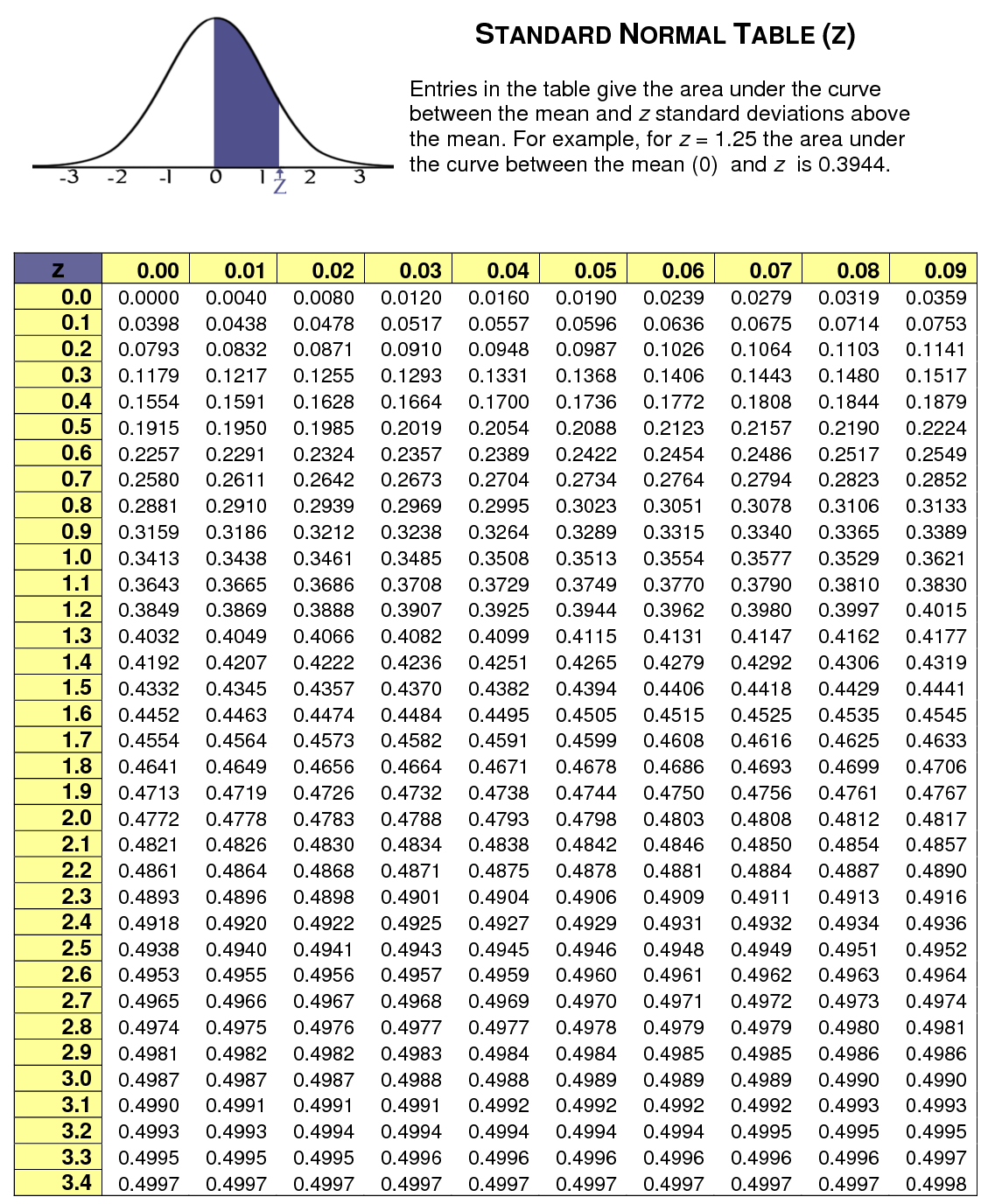
- 보통 어떤 확률변수가 정규분포를 따른다고 할 때, 특정 확률을 구하기 위해 실제로 정규분포를 적분하는 경우는 거의 없다
- 확률변수를 표준화시켜 표준정규분포로 근사시킨 뒤, 표준정규분포표를 보고 확률을 계산한다
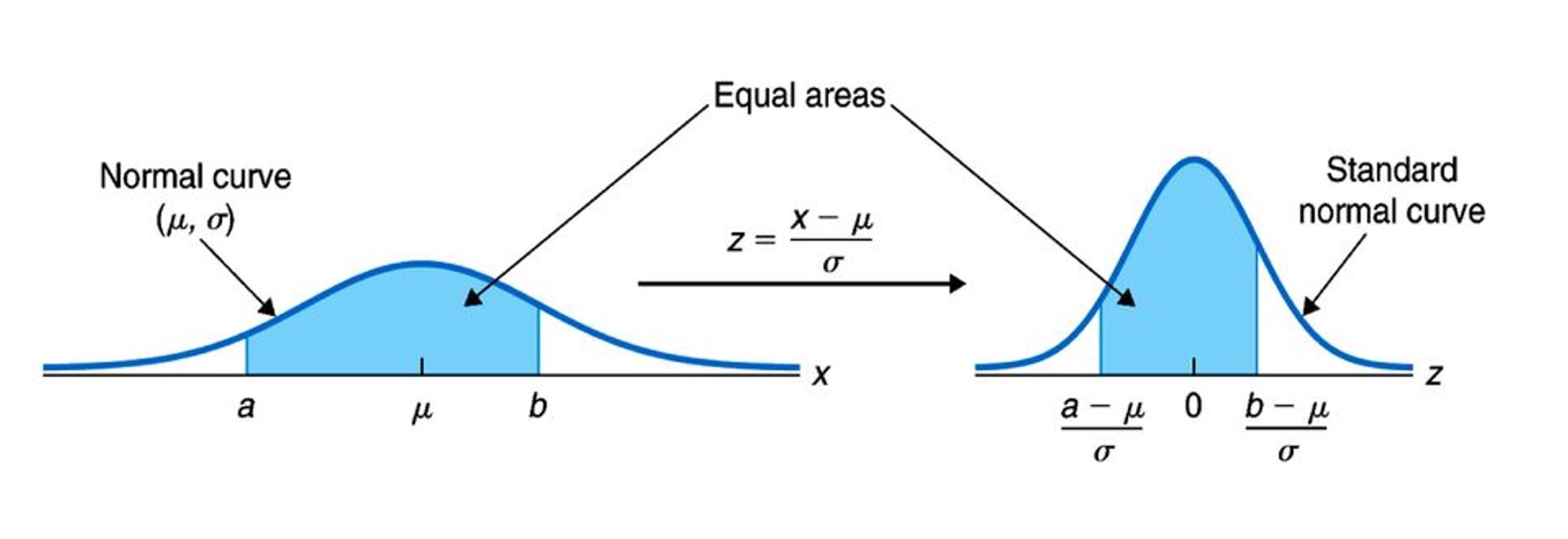
- 분포형태가 달라지는데 굳이 변환을 하는 이유는, 확률 계산을 적분없이 표만보고 하기 위해서다
이항분포를 정규분포로 근사
- n을 늘릴수록 이항분포의 형태는 정규분포와 비슷한 형태가 된다
- n이 크면 이항분포 B(n, p)는 근사적으로 정규분포 N(np, np(1-p))를 따른다
- (성공확률 p가 낮으면 푸아송 분포)
추측 통계
- 모집단 전체를 모두 조사하는 방법을 전수조사(complete survey)라고 한다
- 전체에서 일부를 추출해 얻은 정보를 바탕으로 전체를 추측하는 방법을 표본조사(sample survey)라고 한다
- 모집단에서 일부를 추출할 때 비복원 추출이기 때문에 엄밀하게는 독립적인 시행이라고 할 수 없지만,
-
모집단의 크기가 표본의 크기와 비교해 충분히 큰 경우에는 복원 추출이라고 가정하며 결과적으로 추출을 독립 시행으로 바라본다
- 표본조사를 기반으로 하는 추측 통계 방법은 크게 추정(estimation)과 검정(test)으로 나뉜다
- 추정: 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
- 점추정(point estimation): 표본 조사 결과를 가지고 모집단의 평균과 분산과 같은 값을 한 값으로 추정하는 경우
- 구간추정(interval estimation): 평균과 분산과 같은 값의 폭을 추정하는 경우
- 검정: 표본을 토대로 모집단에 관한 가설을 세우고 참, 거짓을 판별하는 방법
- 추정: 모집단에서 추출한 표본을 이용해 모집단의 모수(평균값, 표준편차 등)를 확률적으로 추측하는 방법
모집단과 표본
- 모집단의 어떤 변량에 관한 분포를 모집단 분포라하고, 모집단 분포를 특징짓는 상수를 모수(모평균, 모분산, 모표준편차 등)라고 한다
- 모집단에 관한 정보는 이미 확정되어 있다
- 표본집단은 일반적으로 매번 다르다. 그래서 E(X)도 일반적으로 매번 다르다
- E(X)는 ∑(Xk*pk) 이므로 E(X)도 확률변수가 될 수 있다
표본평균의 평균과 표준편차
- 표본평균의 평균, 분산 그리고 표준편차는 아래와 같다
- 표본 크기 n이 커질수록 표본평균의 표준편차가 작아진다
- (모집단에서 추출을 충분히 많이 하면, 표본의 평균이 표본집단마다 거의 같아진다는 의미이다)
- (m은 모평균, σ는 모표준편차)
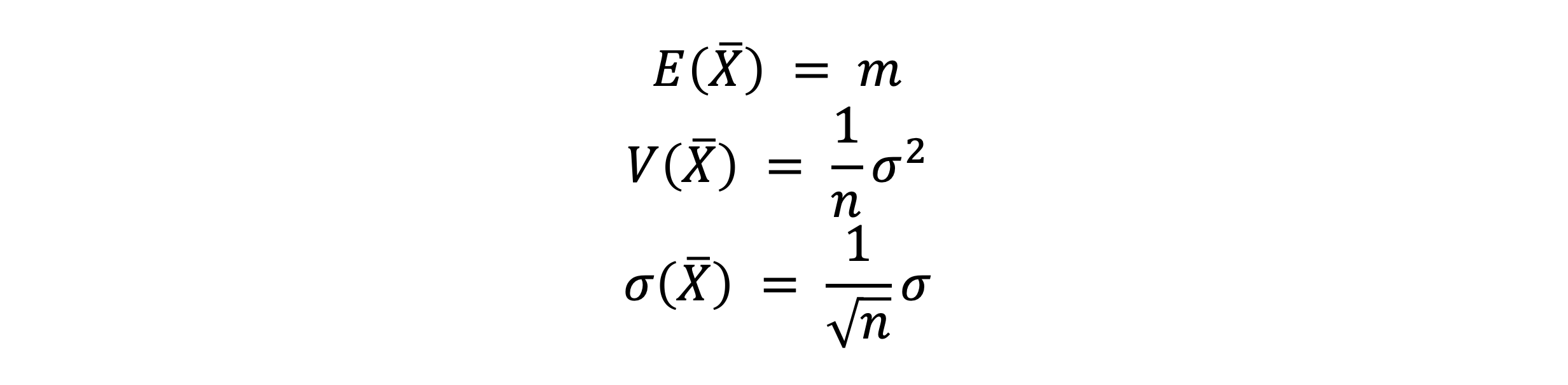
- 우리의 목표는 어디까지나 모집단을 예측하는 것이다
- 위의 식을 보면 표본평균의 평균과 표준편차는 모집단의 평균 표준편차와 밀접한 관계가 있음을 알 수 있다
- 그렇기 때문에 표본을 조사하는데 의미가 있고 추정이 가능한 것이다
큰수의 법칙
- 발생확률이 수학적으로 p인 사건을 반복 시행할 때, n이 작으면 경험적 확률과 수학적 확률간의 차이가 크다
- 하지만 반복시행의 크기 n이 커지면, 경험적 확률이 수학적 확률에 수렴하게 된다(한없이 가까워진다)
- 모집단에 빨간색이 700개, 파란색이 300개 있었다면, 표본의 크기가 커질수록 표본집단에도 빨간색이 70%, 파란색이 30% 비율로 있게 된다
- 큰 수의 법칙: 표본의 크기가 커질수록 표본평균 E(X)는 모평균 m에 가까워진다
- (표본의 크기가 크면 클수록 해당 표본에서 구한 평균이 실제 모평균일 가능성이 높아진다)
중심극한정리
- 표본평균은 기대값 m, 분산이 σ2/n 인 정규분포를 근사적으로 따른다
- 중심극한정리는 큰수의 법칙 내용을 포함하는 정리 (큰 수의 법칙을 보다 정밀하게 표현한 정리)
- 모집단이 어떤 분포라도 표본평균의 분포는 정규분포로 가까워진다