![[AI Basic] 분류](/images/ai_basic_logo.png){kind=logo}
Table of Contents
분류(Classification)
- 분류는 강아지와 고양이와 같은 이중 분류(Binary classification) 또는 자동차, 비행기, 배와 같은 다중 분류(Multi class classification)로 구분된다
- 회귀 모델과 거의 비슷하다. 다른 점은 출력층에 이중 분류는 시그모이드(sigmoid) 함수, 다중 분류는 소프트맥스(softmax) 함수를 사용해, 출력값을 각 클래스가 될 확률로 바꿨다는 점이다
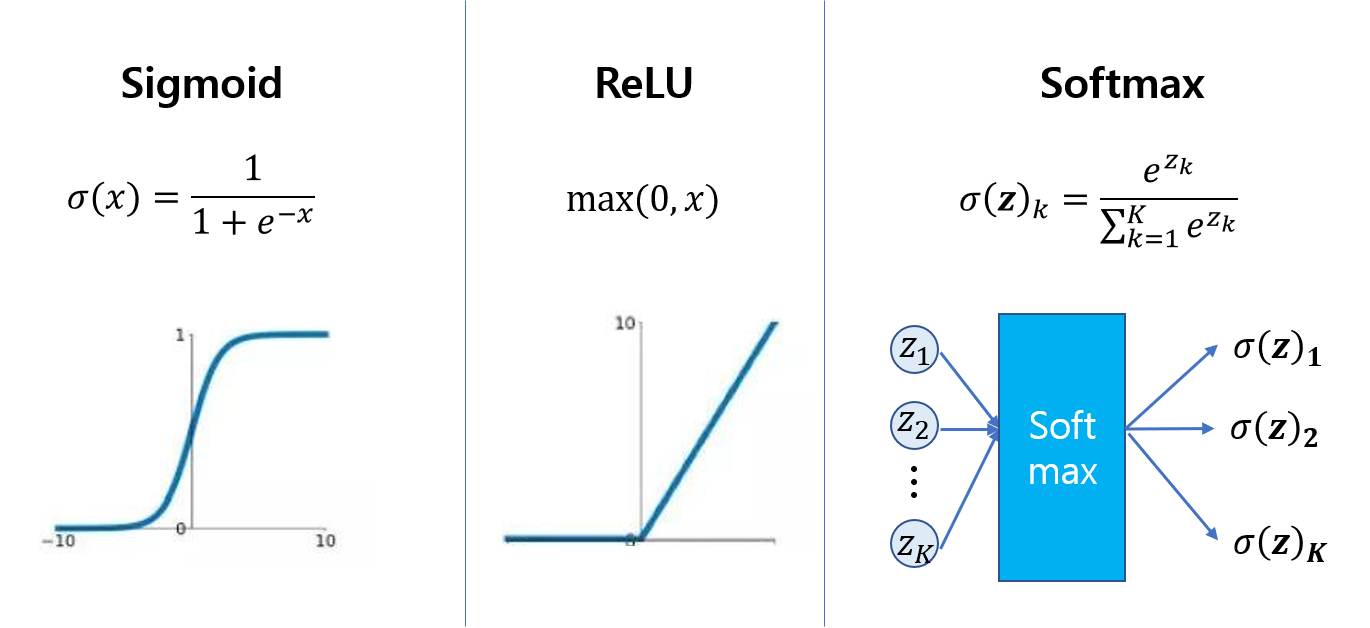
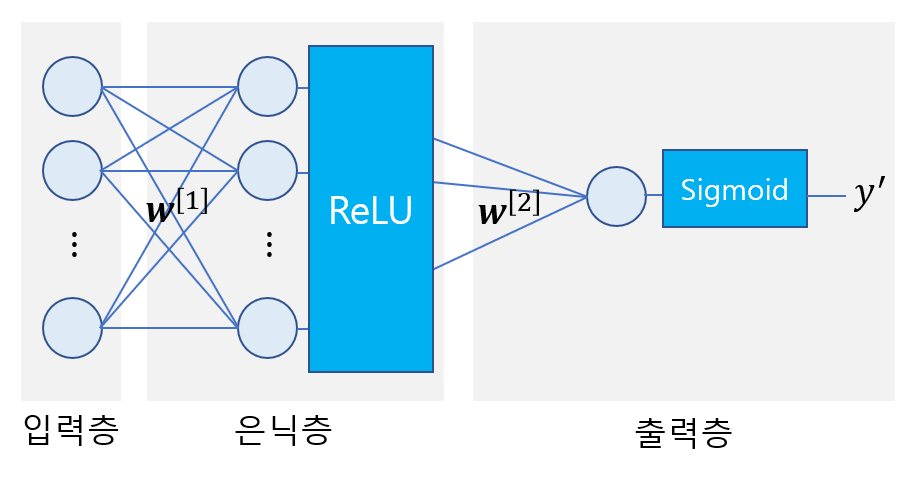
- 보통 은닉층에는 ReLU 함수, 이진 분류의 출력층에는 Sigmoid 함수, 다중 분류의 출력층에는 Softmax 함수를 쓴다
손실 함수
- 분류 문제는 출력층이 특정 클래스가 될 확률 값이다
- 확률 값을 출력으로 할 때 손실 함수는 어떻게 정의하는게 좋을까?
-
회귀 문제에서의 MSE 손실함수는, 타겟 값의 확률은 1, 타겟이 아닌 값의 확률은 0으로 동시에 보낼 수 없다
- 타겟 값(p)이 1일 때 확률(q)를 최대로 하고, 타겟 값이 0일 때 확률을 최소로 하자
- 이러한 로직을 의사(Pseudo) 코드로 나타내보면 아래와 같다
p: 예측할 값 (ex. 0 또는 1)
if p == 1:
q 를 최대화
else if p == 0:
q 를 최소화 (-q를 최대화 -> 1-q를 최대화)
- 이를 하나의 값으로 축약하면 아래와 같다
- 이 값은 곧 Likelihood를 의미한다
- 그래서 결국 분류 문제는 최대우도추정(MLE)을 하는 것과 같다
- 하지만 확률은 0과 1사이의 값이기 때문에 여러 데이터에 대해 최대우도추정을 하기에는 그 값이 계속 작아진다
- 또 모델 학습에서 비용 함수(Cost function)은 무엇인가를 최소화하는 것이 일반적이다
- 그래서 아래와 같은 과정을 추가한다
- 위의 파란색을 음의 Log likelihood 값이라 하고 이를 크로스 엔트로피라고 한다
- 결국 비용함수는 크로스 엔트로피이고, 분류문제는 크로스 엔트로피를 최소로 하도록 한다
- 이 비용함수에 대한 정규방정식은 없지만, convex function이라서 경사하강법을 이용하면 해(모델 파라미터)를 구할 수 있다