딥러닝 성능 향상을 위한 요령

딥러닝 성능 향상의 방향성

과잉 적합 방지를 통한 일반화 능력 극대화 (실전에 배치되었을 때의 성능을 극대화)
학습 알고리즘의 속도 향상 (더 빠른 학습은 결국 더 좋은 성능을 가져다 준다)

데이터 정규화

데이터가 양수, 음수 값을 골고루 갖도록 한다 => 평균: 0
특성 scale이 같도록 한다 => 표준편차: 1

가중치 초기화(Initialization)

역전파 알고리즘은 출력층에서 입력층으로 오차 그래디언트를 전파하면서 진행된다. 그런데 알고리즘이 하위층으로 진행될수록 그래디언트가 작아지는 경우가 많다. 이 문제를 그래디언트 소실이라고 한다. 어떤 경우엔 반대로 그래디언트가 점점 커져 여러 층이 비정상적으로 큰 가중치로 갱신되면 알고리즘은 발산한다. 이 문제를 그래디언트 폭주라고 하며 순환 신경망에서 주로 나타난다. 일반적으로 불안정한 그래디언트는 심층 신경망 훈련을 어렵게 만든다. 층마다 학습 속도가 달라질 수 있기 때문이다.

기계 학습 초기에는 가중치 초기화를 정규분포 형태(평균:0, 분산:1)를 갖도록 초기화하였다. 하지만 입력층의 노드 수가 많다면 출력층의 분포는 밑에 그림과 같이 값들이 대부분 0이나 1로 수렴하게 된다. 문제는 0과 1근처에서 활성화 함수의 그래디언트가 거의 0에 가깝다는 것이다. 그렇기 때문에 아래층까지 역전파가 진행되기도 전에 이미 그래디언트가 거의 소실된다.

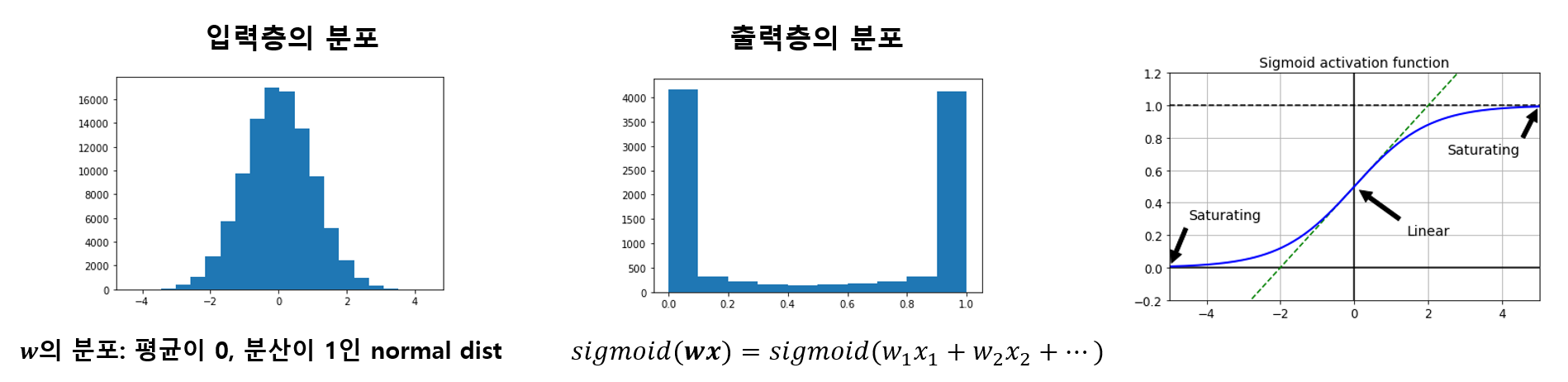
그렇다면 출력층의 분포가 어떤게 좋을까? 출력층의 값이 고르게 분포해 시그모이드 함수의 비선형성과 적당한 그래디언트를 갖도록 하는 것이 좋을 것이다.

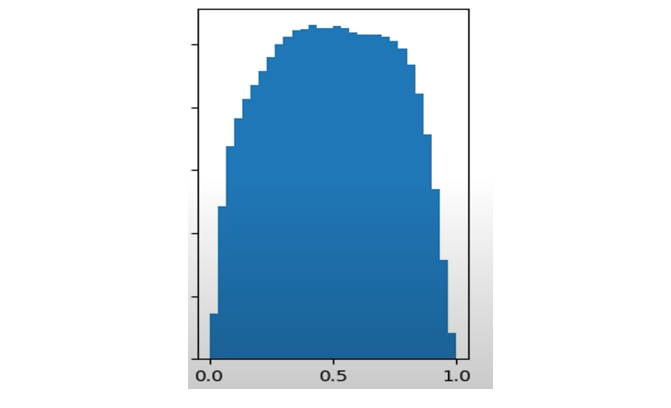
그렇다면 왜 이런 분포가 안되는 걸까? 아마 그 이유는 입력층(각 층은 다음 층의 입력층이므로 결국 모든 층)의 노드 수가 많으면 가중치와 데이터가 정규분포를 갖는다고 하더라도 모두 더하게 되면 출력층에 sum(wx)의 값이 치우치게 되고 그러면 sigmoid(sum(wx))는 0또는 1로 주로 분포하게 될 것 이다. 따라서 이를 완화시켜주기 위해서는 입력층의 노드 수가 많다면 그만큼 가중치의 분산을 작게 하여 최대한 작은 값을 갖도록 하면 sum(wx)의 값이 치우치게 되지 않도록 해줄 것이다. 이와 관련한 몇 가지 초기화 방법을 살펴보자.

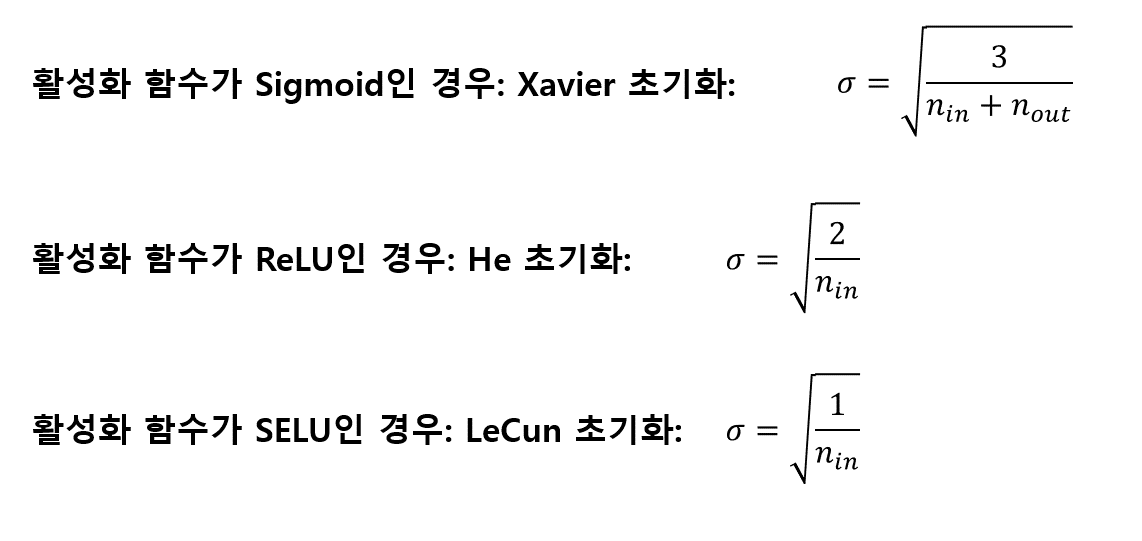
🔔 가중치 초기화는 Gradient vanishing문제를 완화시켜준다.

평균이 0인 정규 분포를 갖도록 한다
표준편차 크면 그리고 노드의 갯수도 많으면 값이 특정 부분에 몰리게 된다.

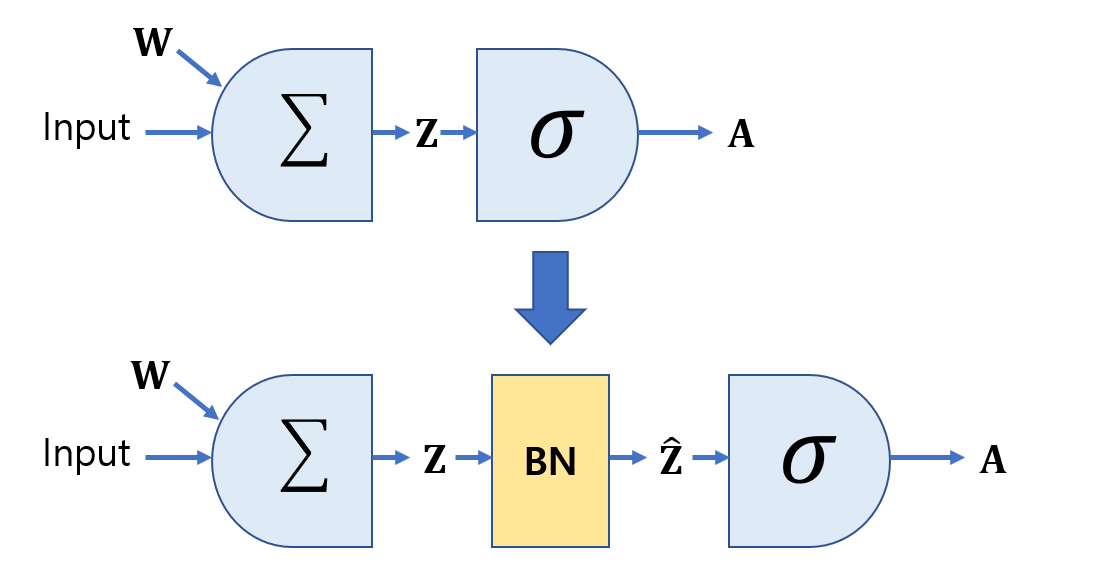
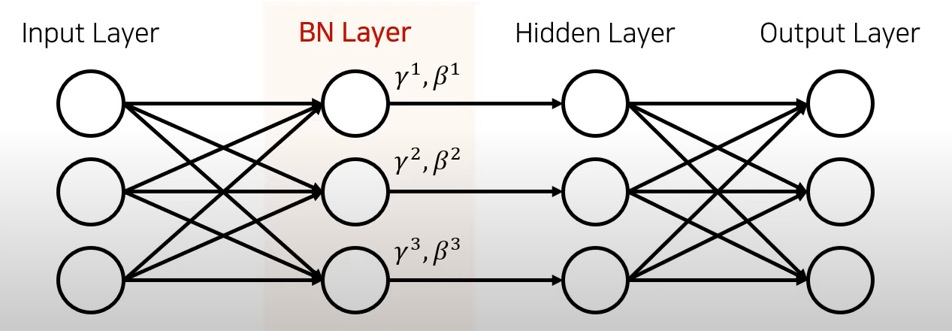
배치 정규화(Batch Normalization)

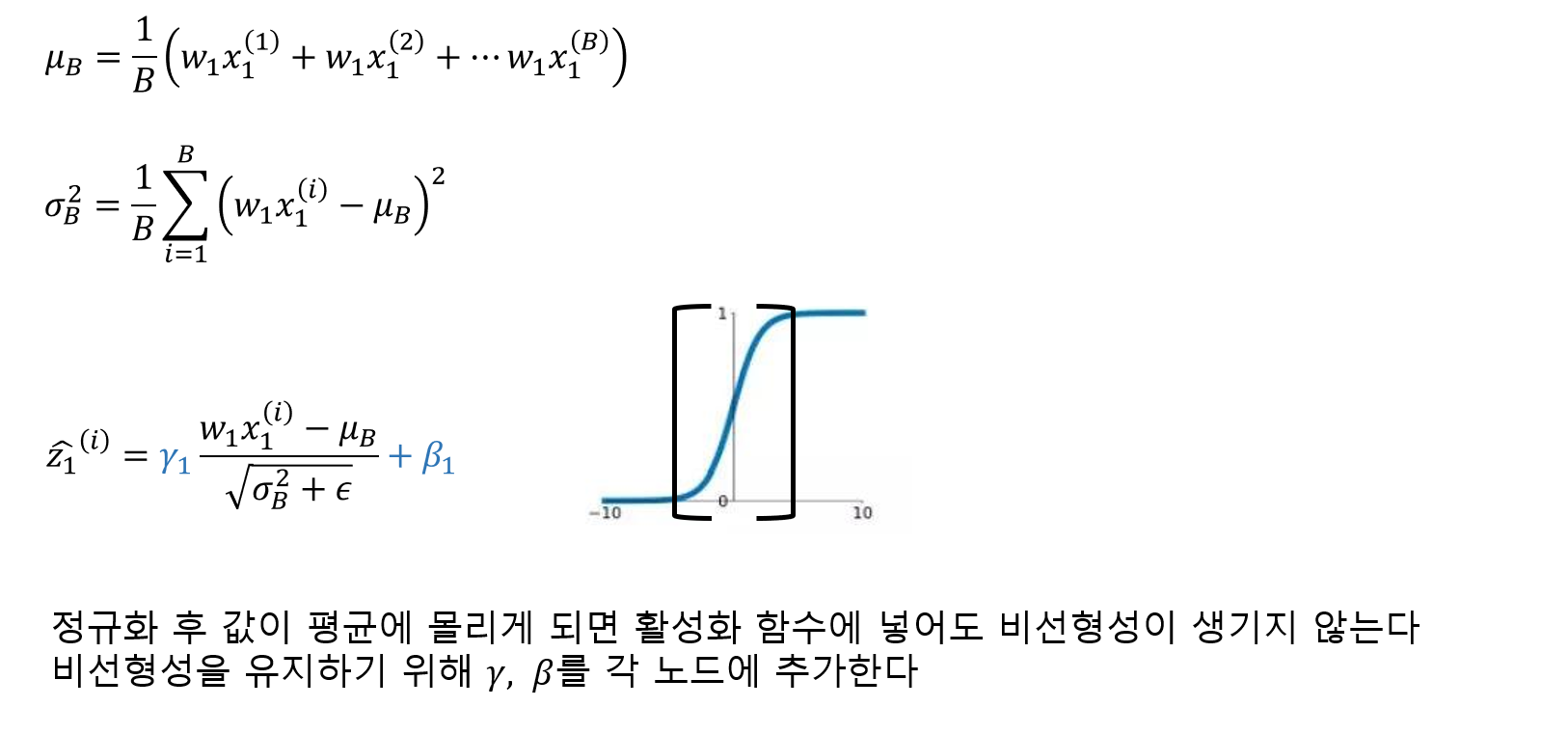
배치 정규화는 각 층에서 활성화 함수를 통과하기 전이나 후에 입력을 정규화한 다음, 두 개의 새로운 파라미터(𝛾, 𝛽)로 결과값의 스케일을 조정하고 이동시킨다. 정규화 하기 위해서는 평균과 표준편차를 구해야 한다. 이를 위해 현재 미니배치에서 입력의 평균과 표준편차를 평가한다. 테스트 시에는 어떻게 할까? 간단한 문제는 아니다. 아마 샘플의 배치가 아니라 샘플 하나에 대한 예측을 만들어야 한다. 이 경우 입력의 평균과 표준편차를 계산할 방법이 없다. 샘플의 배치를 사용한다 하더라도 매우 작거나 독립 동일 분포(IID)조건을 만족하지 못할 수도 있다.

딥러닝에서는 이를 층의 입력 평균과 표준편차의 이동 평균(moving average)을 사용해 훈련하는 동안 최종 통계를 추정함으로써 해결한다.

정리하면 배치 정규화 층마다 네 개의 파라미터 벡터가 학습된다. 𝛾(출력 스케일 벡터)와 𝛽(출력 이동 벡터)는 일반적인 역전파를 통해 학습된다. 𝜇(최종 입력 평균 벡터)와 𝜎(최종 입력 표준편차 벡터)는 지수 이동 평균을 사용하여 추정된다. 𝜇와 𝜎는 훈련하는 동안 추정되지만 훈련이 끝난 후에 사용된다.(배치 입력 평균과 표준편차를 대체하기 위해)

배치 정규화는 다음과 같은 이점이 있다

Gradient vanishing문제를 완화시켜준다
Learning rate 높여도 학습이 잘된다
일반화 능력이 좋아진다

그래디언트 모멘텀(Gradient Momentum)

모멘텀은 학습을 좀 더 안정감 있게 하도록 해준다. 데이터에 의해 Gradient를 계산할 때 만약 Noisy한 데이터인 경우, Gradient가 잘못된 방향으로 갈 가능성이 크다. 그렇기 때문에 그 동안 누적된 Gradient를 감안하여 Gradient가 Noisy한 데이터에 의한 안 좋은 영향을 줄여준다.

Momentum method can accelelerate gradient descent by taking accounts of previous gradients in the update rule equation in every iteration

적응적 학습률(Adaptive Learning-rate)

가중치 업데이트의 척도가 되는 학습률을 각 가중치의 학습 진행 정도에 따라 다르게 바꿔주는 것을 적응적 학습률이라고 한다. 예를 들어, 가중치의 업데이트가 많이 이루어질수록 점점 학습률을 줄여나간다. 또 특성마다 업데이트가 많이 된 특성은 학습률을 줄이고, 적게된 특성은 학습률을 늘린다.