Table of Contents
CNN 등장 배경
- 노드가 서로 완전 연결되어 있는 완전 연결층(Fully Connected Layer)은 가중치가 너무 많다는 단점이 있다
- 가중치가 너무 많으면 학습 속도를 더디게 하고, 또한 과잉적합에 빠질 가능성을 높이게 된다
- 예를 들어, 이미지는
가로 * 세로 * RGB채널 이라는 3차원의 데이터로 표현되는데,256 * 256짜리 이미지를 생각하면256 * 256 * 3 = 196,608개의 엄청난 사이즈를 가지는 데이터라고 할 수 있다 - 이러한 이미지를 단순히 완전 연결층 모델로 이진 분류(ex. 개, 고양이 사진) 한다고 하면, 크게 두 가지 문제가 있다
- 196,608개의 입력, 2개의 출력을 가지는 단순 선형 레이어라고 해도 약 40만개라는 엄청난 숫자의 가중치가 필요하다
- 이미지를 단순히 1차원으로 늘린다면 이미지라는 공간적 특성(spatial structure)이 모두 사라지게 된다
- 이러한 문제를 해결하기 위해 컨볼루션 신경망(Convolutional Neural Network)이 등장했다
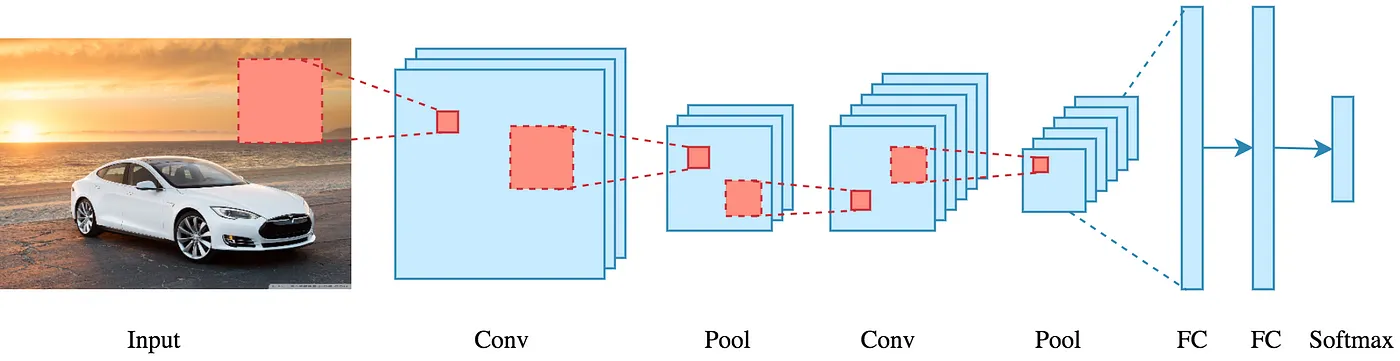
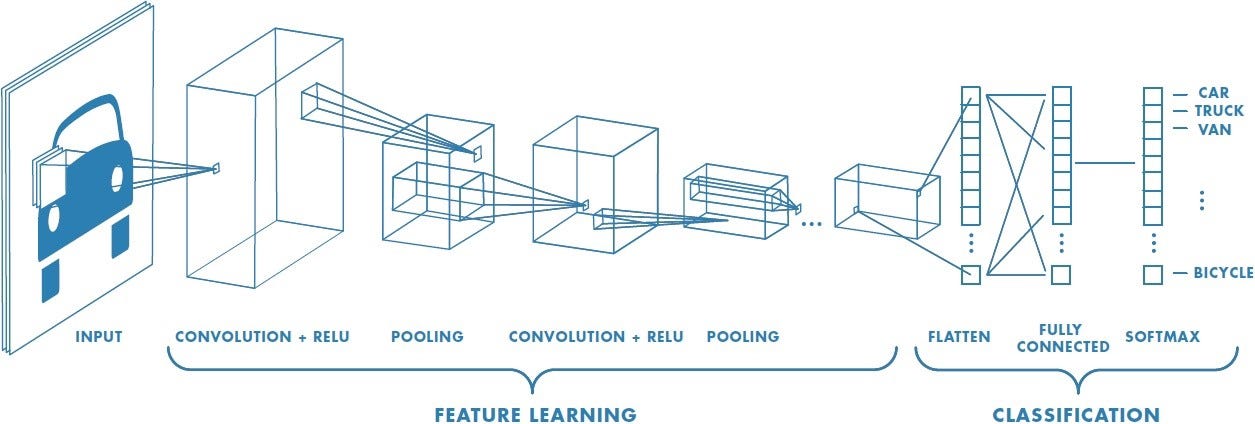
CNN
- 컨볼루션 신경망(CNN: Convolutional Neural Network)
- CNN은 크게 컨볼루션 연산 계층, 풀링 연산 계층으로 이루어진다
- 컨볼루션 신경망은 입력의 공간적 특성(spatial structure)을 활용하며, 가중치의 숫자를 획기적으로 줄여준다는 장점이 있다
컨볼루션 연산
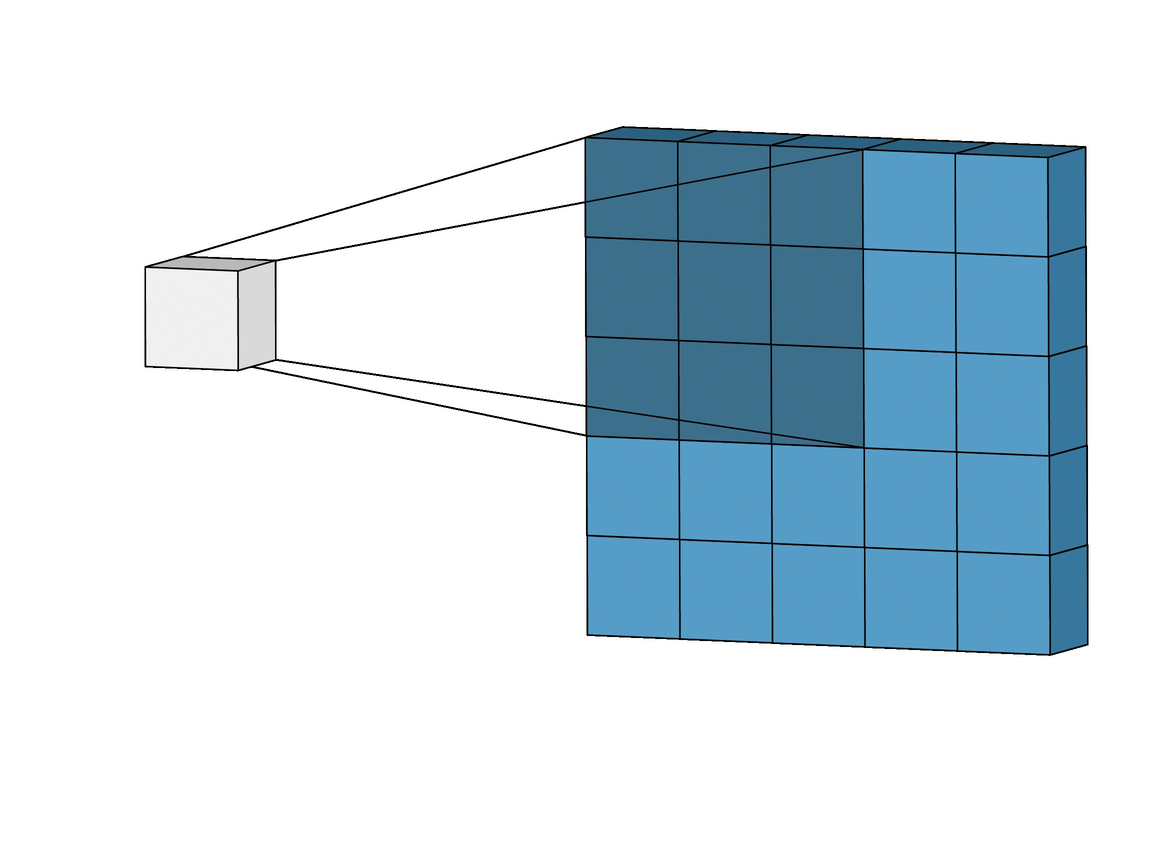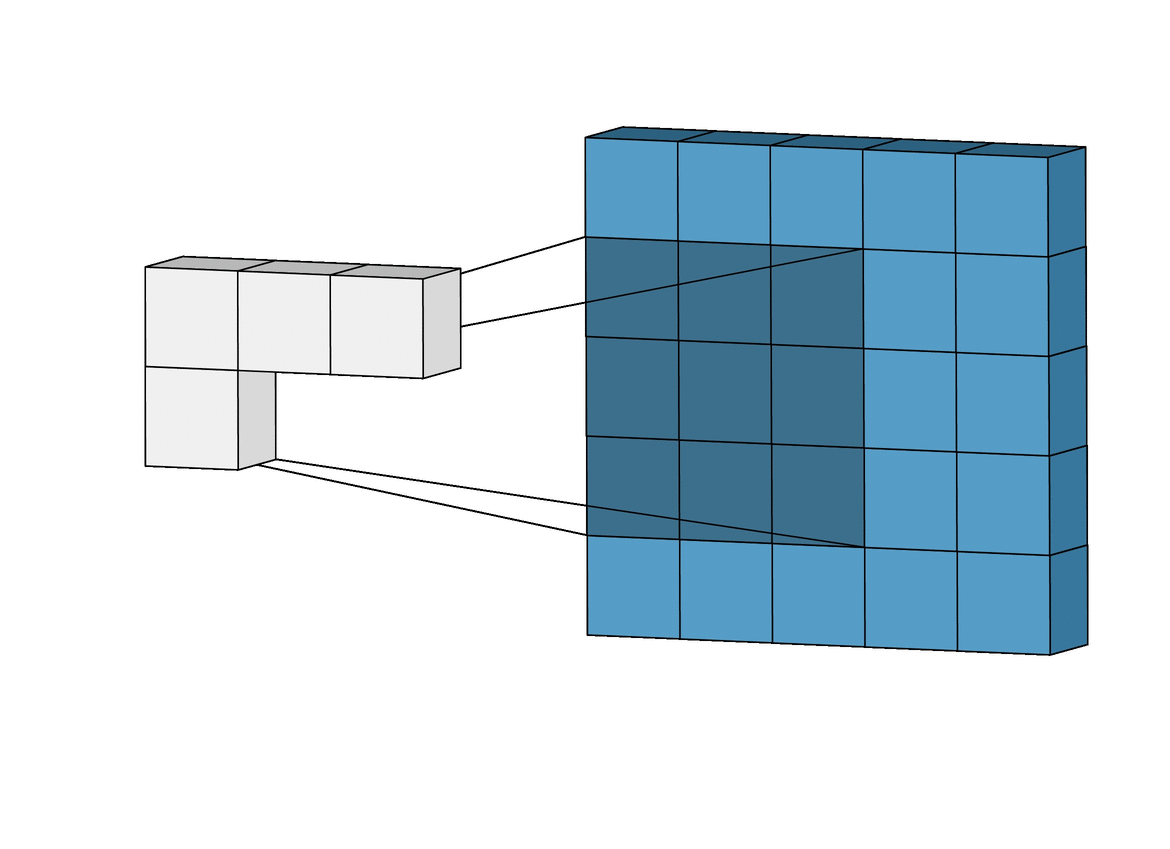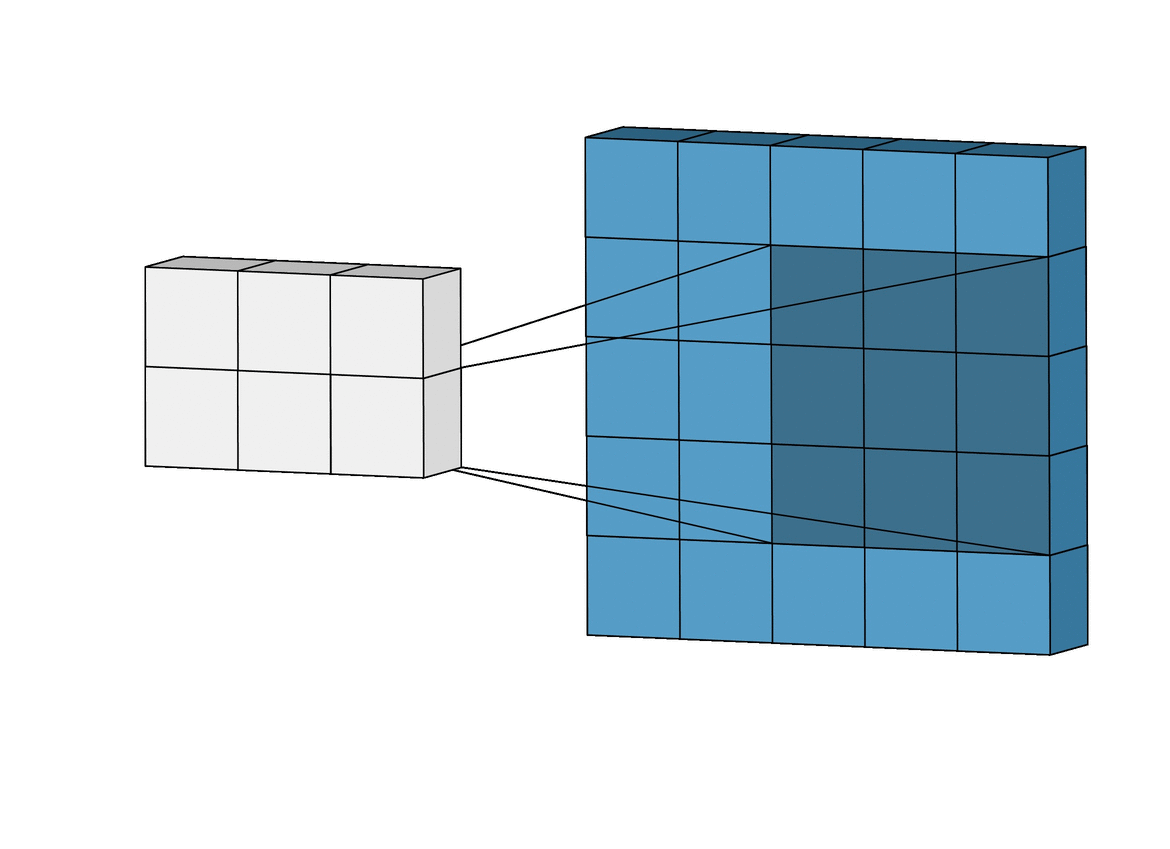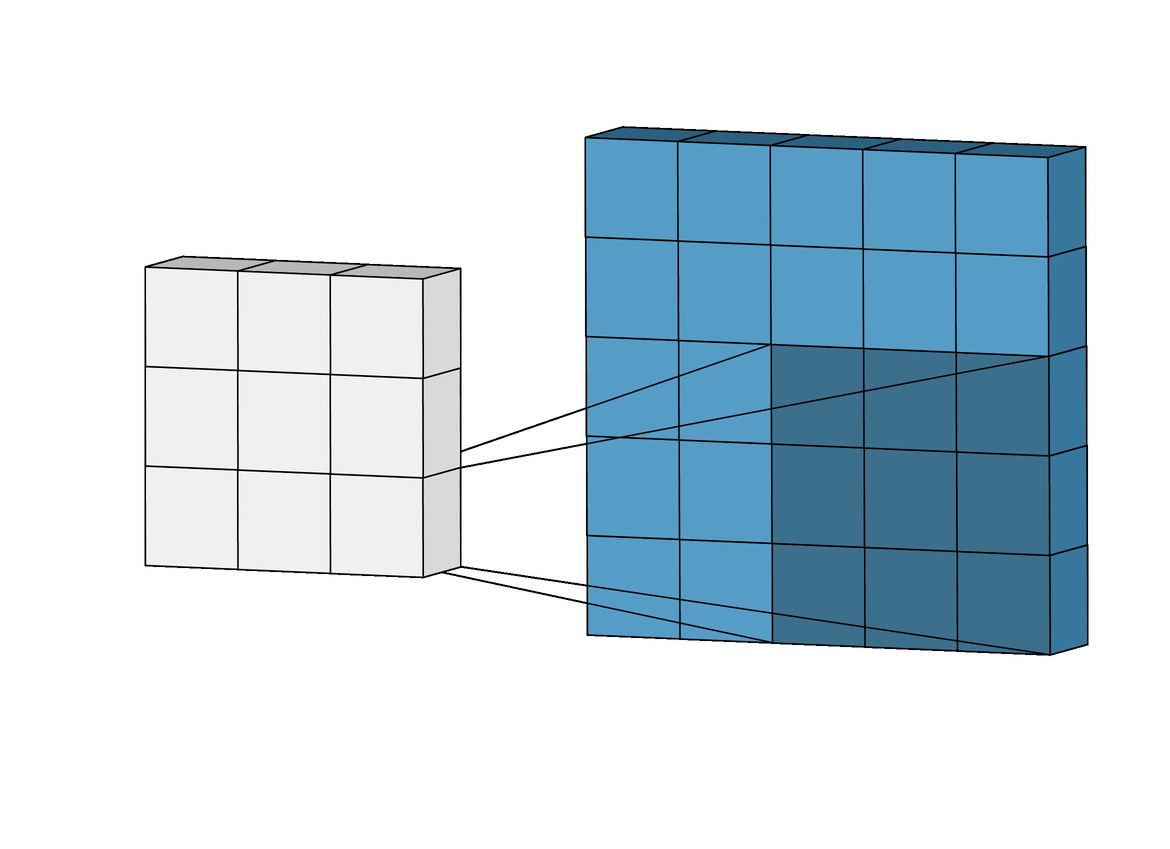
- 컨볼루션 연산은 적당한 크기의 필터가 입력을 좌측 상단에서 우측 하단으로 슬라이딩하며 입력과 필터를 원소간 곱(element-wise product)한 후 더하는 연산을 말한다
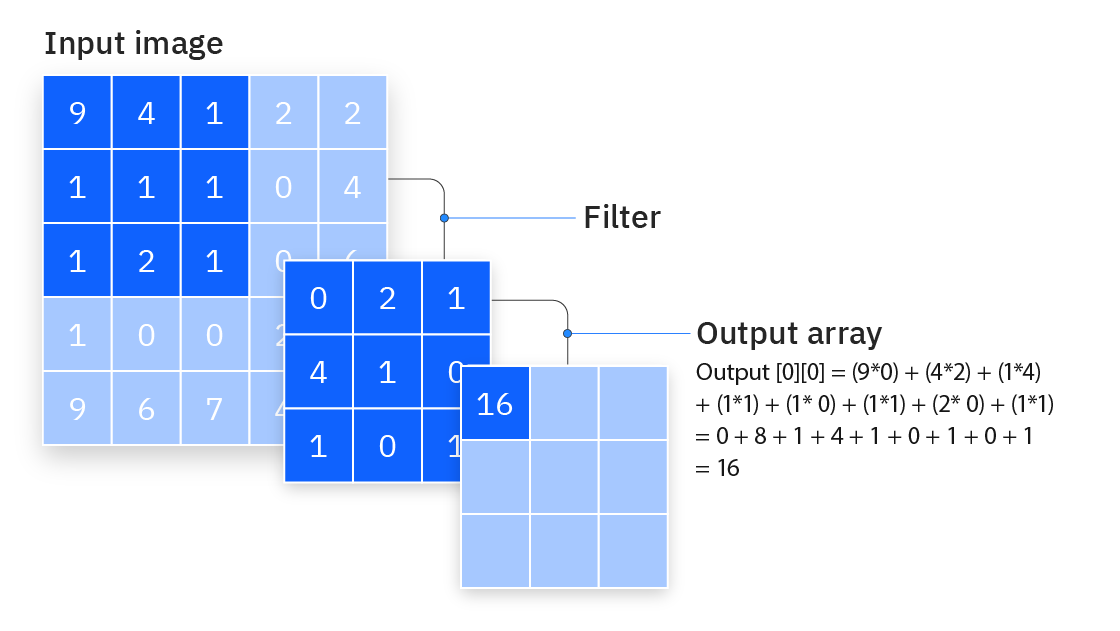
필터
- 컨볼루션 연산에 사용되는 필터가 CNN 에서 학습하는 가중치를 갖는 주인공이다
-
다시 말해 CNN 모델이 데이터를 통해 학습하는 가중치가 바로 필터가 가지고 있는 파라미터 값을 의미한다
- 위 그림에서는 필터가 가로와 세로만 있는 것처럼 묘사됐지만 항상 그렇지는 않다
- 예를 들어, 컬러 이미지의 경우 RGB 라는 3개의 채널을 가진다
- 그러면 필터도 마찬가지로 3차원 형태가 된다. 일반식으로 표현하면
(k * k * C)이다 (k: 커널의 크기,C: 채널 수) -
필터는 (k * k) 형태의 커널을 채널 수(C) 만큼 쌓은 형태라고 생각하면 된다
-
예를 들어 채널이 1(Gray scale)이고 필터가 두 개인 경우 그림은 다음과 같다
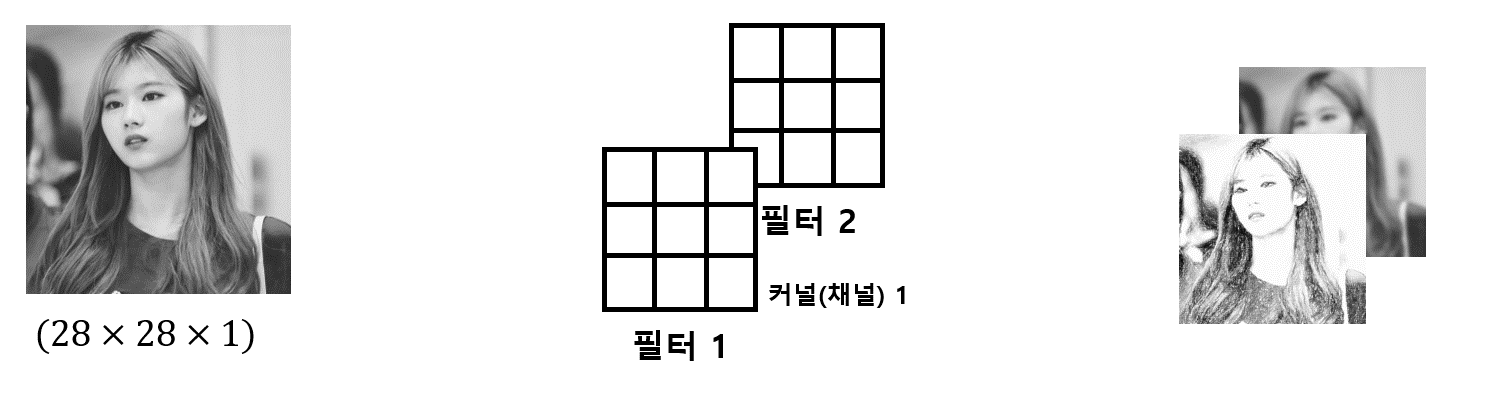
-
만약 채널이 3(RGB scale)이고 필터가 두 개인 경우 그림은 다음과 같다
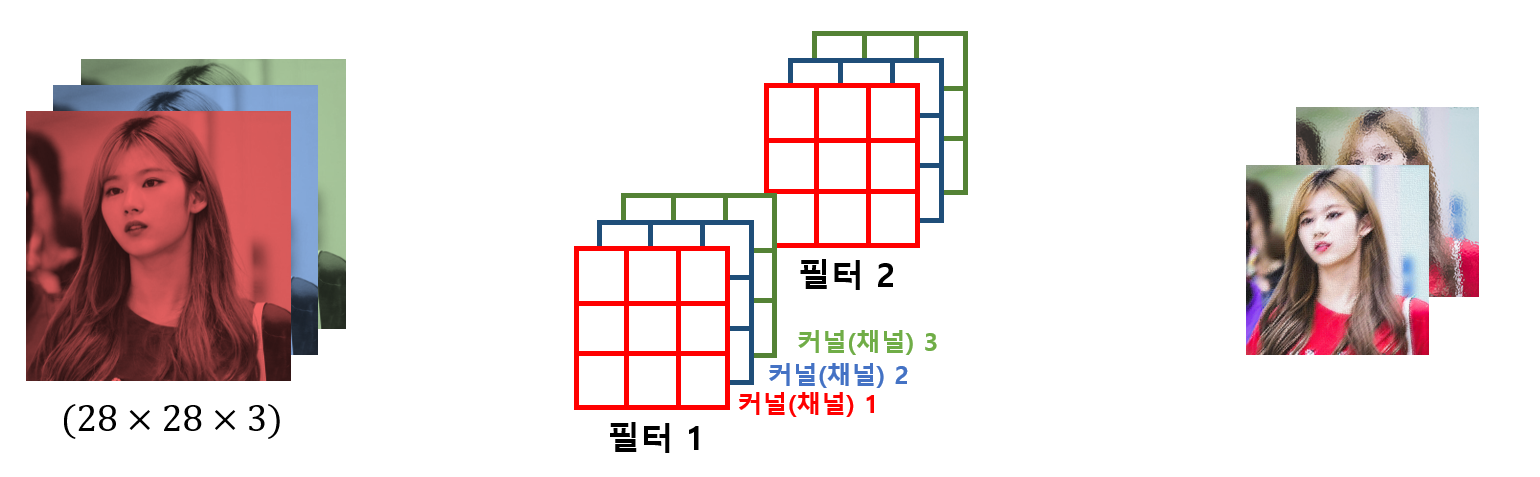
- 필터는 입력 데이터의 특성을 잘 추출한다
- 예를 들어, 어떤 필터는 데이터의 윤곽을 추출하는 역할, 둥근 부분을 추출하는 역할 등 이렇게 필터마다 데이터의 다양한 특성을 추출하는 역할을 한다
- (사람의 얼굴 이미지를 통해 나이를 추측하기 위해 ‘주름’이라는 특성을 추출하는 필터가 있을 수 있다)
- (개와 고양이를 분류하기 위해 고양이한테 많이 있는 줄무늬 형태의 털을 추출하는 필터가 있을 수도 있다)
- CNN에서 필터가 데이터의 어떤 특성을 추출할지는 학습을 통해 정해진다. 사람이 임의로 결정하는 것이 아니다
- (그것이 인공지능이니까)

- 여기서 잠깐 파이토치에서 컨볼루션 연산 레이어를 어떻게 만들고, 이 때 가중치의 개수를 어떻게 구하는지 실습해보자
- 파이토치의
torch.nn.Conv2d클래스를 이용한다. 사용되는 필수 인자를 간단히 설명하면,in_channels- 입력 데이터의 채널 수
- (RGB 컬러 이미지의 경우 3)
out_channels- 사용할 필터의 수
- 동시에 출력 데이터의 채널 수이기도 하다
- 사용된 수만큼 다양한 피처맵이 생성되지만, 너무 많으면 가중치 늘어남
kernel_size- 커널의 가로, 세로 크기
- 예를 들어,
Conv2d(3, 6, 16)인 경우(16 * 16 * 3)짜리 필터를 6개 사용하므로16 * 16 * 3 * 6 = 4,608개의 가중치를 학습해야 한다 - (그리고 필터 6개 만큼의 바이어스 값 6개도 있으므로 정확히는 4614개)
import torch.nn as nn
from torchinfo import summary
conv = nn.Conv2d(3, 6, 16)
summary(conv)
----------------------------------------------------------
=================================================================
Layer (type:depth-idx) Param #
=================================================================
Conv2d 4,614
=================================================================
Total params: 4,614
Trainable params: 4,614
- 필터는 중요하기 때문에, 마지막으로 정리하자면 다음과 같다
- CNN에서 학습하는 가중치가 바로 필터의 파라미터 값이다
- 필터는 (k * k) 형태의 커널을 채널 수(C) 만큼 쌓은 형태
- 필터의 수가 출력 데이터의 채널 수
- 필터는 입력 데이터의 특성을 잘 추출한다. 그래서 출력 값을 피처맵(Featured map)이라고 한다
풀링
- 풀링층은 특성 맵의 사이즈를 줄여주는 역할을 한다
- 보통 최대 풀링 또는 평균 풀링을 많이 사용한다
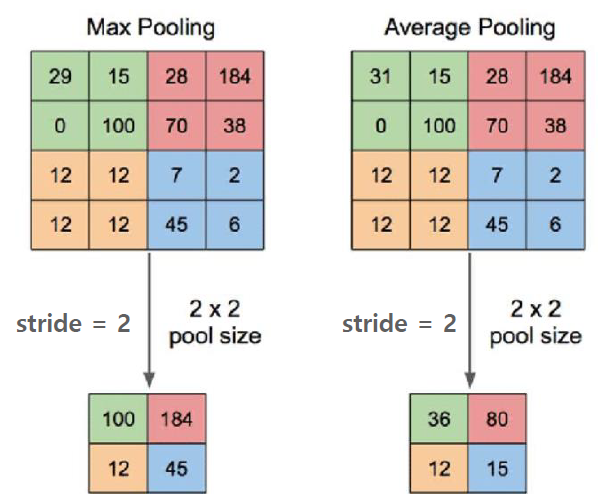
- 보통은 Conv연산, ReLU activation함수를 적용한 후에 풀링을 적용한다
스트라이드, 패딩
스트라이드
- 스트라이드는 필터의 미끄러지는 간격을 조절하는 것을 말합니다.
- 기본은 1이지만, 2를(2pixel 단위로 Sliding window 이동) 적용하면 입력 특성 맵 대비 출력 특성 맵의 크기를 대략 절반으로 줄여줍니다.
- stride 를 키우면 공간적인 feature 특성을 손실할 가능성이 높아지지만, 이것이 중요 feature 들의 손실을 반드시 의미하지는 않습니다.
- 오히려 불필요한 특성을 제거하는 효과를 가져 올 수 있습니다. 또한 Convolution 연산 속도를 향상 시킵니다.
패딩
- 패딩은 데이터 양 끝에 빈 원소를 추가하는 것을 말합니다.
-
패딩에는 밸리드(valid) 패딩, 풀(full) 패딩, 세임(same) 패딩이 있습니다. 패딩 각각의 역할은 다음과 같습니다.
패딩 역할 밸리드 평범한 패딩으로 원소별 연산 참여도가 다르다 풀 데이터 원소의 연산 참여도를 갖게 만든다 세임 특성 맵의 사이즈가 기존 데이터의 사이즈와 같도록 만든다 - 세임패딩을 적용하면 Conv 연산 수행 시 출력 특성 맵 이 입력 특성 맵 대비 계속적으로 작아지는 것을 막아줍니다.
피처 맵
- CNN 각 계층마다 필터가 있고 필터를 통해 나오는 출력을 피처맵(Featured map)이라고 한다
- 각 계층에서 나오는 피처맵의 형태는 아래와 같다

- 계층을 지날수록 피처맵은 원본 이미지와는 거리가 먼 추상화된 형태로 나타나게 된다
- 그 이유는 처음에는 이미지의 간단한 엣지(edge), 형태(shape)에 초점을 맞추고, 계층을 지날수록 인공지능이 이미지를 분류하는데 직접적으로 필요로 하는 정보와 관련된 형태로 피처맵이 변하게 되기 때문이다
- (사람이 보기에는 잘 모르겠지만 인공지능에게는 굉장히 유용한 형태로)



































![[AI Basic] CNN](/images/ai_basic_logo.png)