Table of Contents
Dijkstra
- 가중치 그래프에서 두 정점간 최단 거리 찾는 알고리즘
- 3개의 변수:
- 거리: 현재까지 얻은 최단거리
- 이전 노드: 내가 어떤 노드를 거쳐 현재의 최단거리를 가지고 있는지 (그래야 최단 거리뿐만 아니라 최단 경로도 알 수 있음)
- 완료 여부: 해당 노드까지의 최단 경로를 찾았다고 표시하기 위한 변수 (완료 표시한 후 해당 노드에서 인접한 노드의 경로를 모두 업데이트)
- Edge Relaxation operation이 핵심 -> ex. A와 C사이의 (최단)거리가 3이었는데 A-B-C 이렇게 B를 거쳐가니 거리가 2다 -> A와 C사이의 (최단)거리가 2다
- 자신의 노드에서 이웃노드까지의 거리를 업데이트(Edge Relaxation). 업데이트 후 다음 방문할 노드는 그 중 가장 짧은 이웃노드로 선택
- 탐욕 알고리즘의 일종이다
- 이러한 탐욕 알고리즘이 어떻게 두 정점간 최단거리 문제의 최적해가 될 수 있을까?
- 이 물음에 대한 해답은 다음 방문할 노드로 가장 짧은 이웃노드를 선택하는 것과 깊은 관련이 있다
- 다음 방문할 노드로 가장 짧은 노드(ex. B)를 선택해야 다음 방문되는 노드(B)까지 올 수 있는 또 다른 최단 경로가 없다는 의미를 가지고, 이러한 의미 덕분에 그 노드(B)를 완료 표시 할 수 있으며, 그래야 이 후 다른 노드(C, D 등)에서 해당 노드(B)를 방문하지 않아도 되는 것이 확실해지기 때문이다
- 관련 문제: Leet Code, Network Delay Time
아래와 같은 그래프를 예로 들어보자.
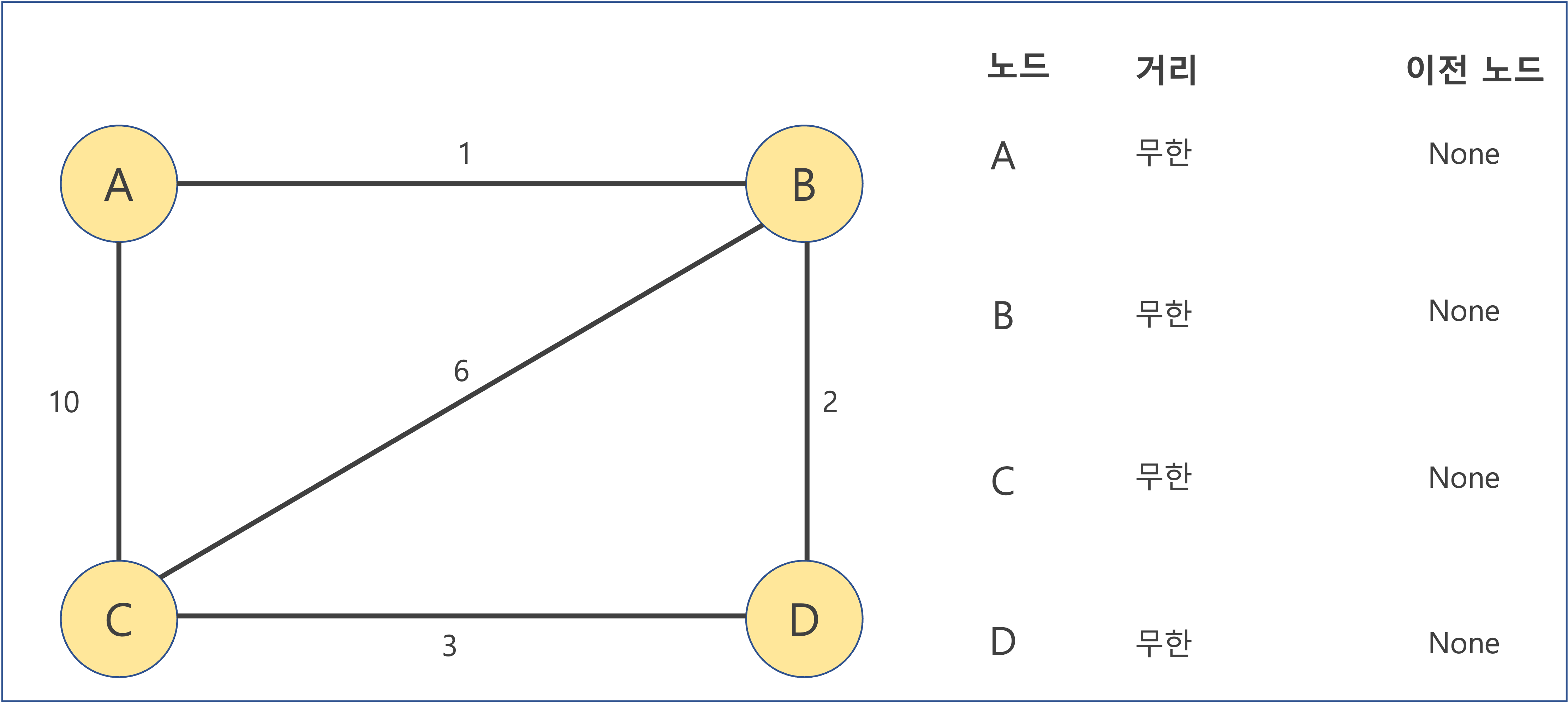
여기서 A에서 C까지의 최단 경로는 A-B-D-C이다.
우선 A를 먼저 완료 표시한 후, 인접 노드를 Edge Relaxation하고나면 다음과 같다.
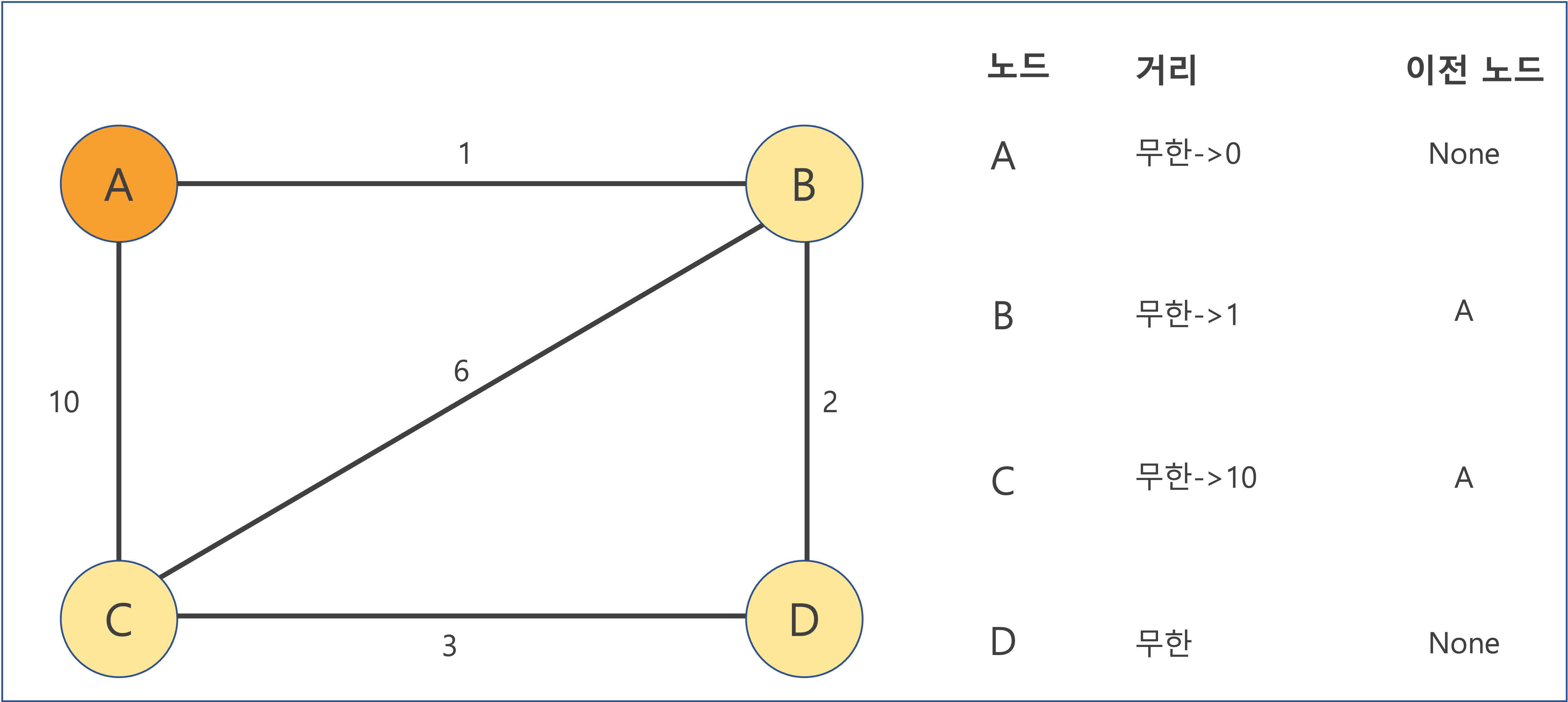
여기서 만약 다음 방문할 노드로 B(현 시점 A에서 가장 가까운 노드)가 아닌 C를 방문한다고 해보자.
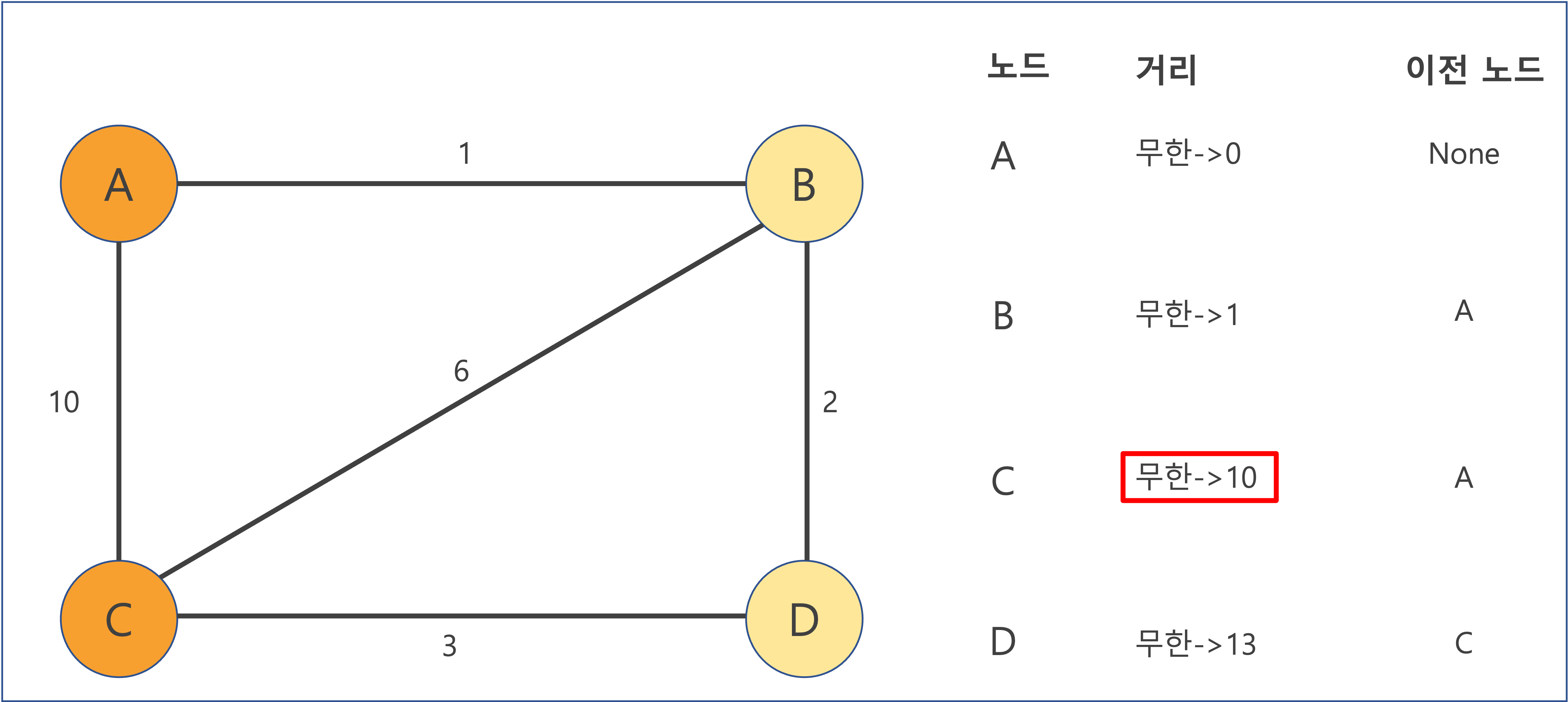
여기서 C에 도착해서 우선 완료 표시를 하게 되는데 여기서 잘못된다. -> C로 올 수 있는 더 짧은 경로가 있는데도 완료 표시를 하게 된다.
다시 돌아가서 Dijstra 알고리즘 대로 현 시점 A에서 가장 가까운 노드인 B를 선택한다면,
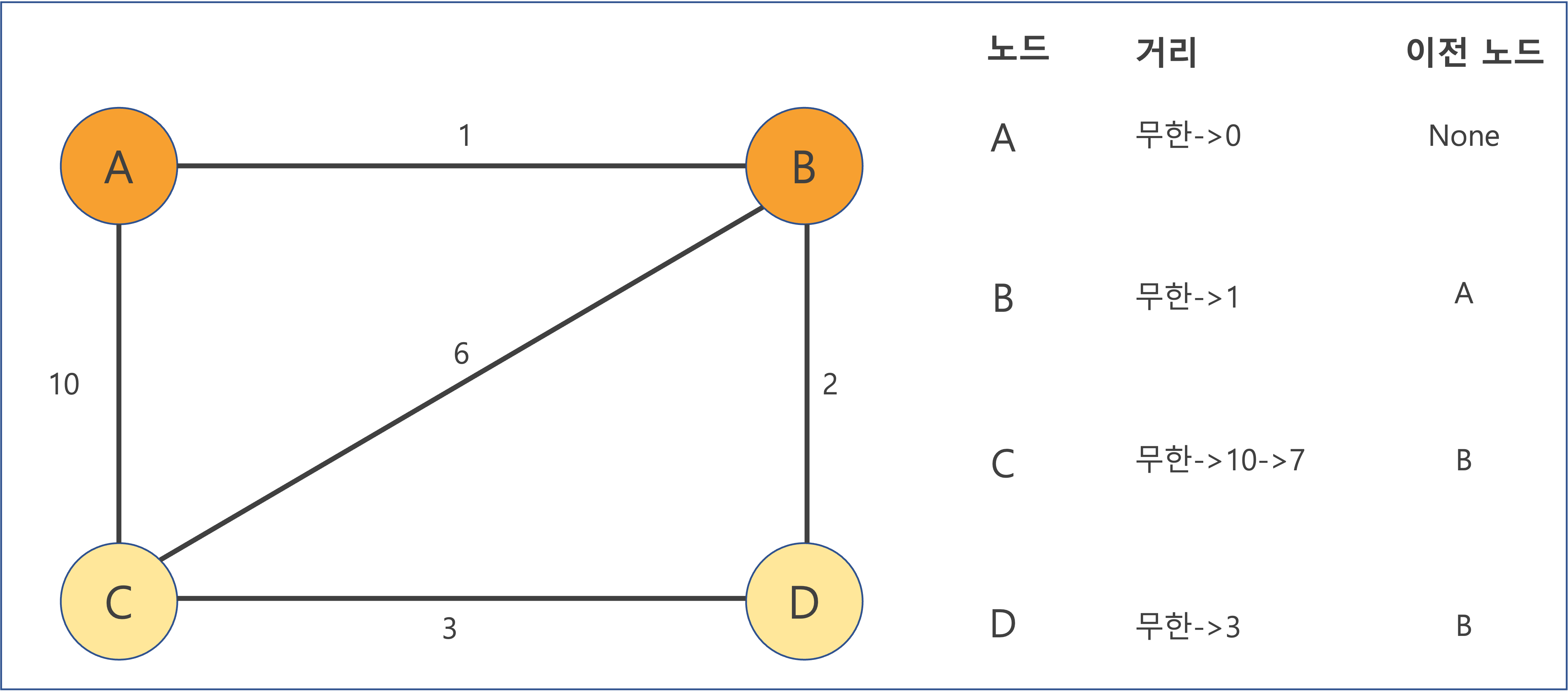
A에서 B로 가는 경로는 더 짧은 경로가 없다는 것을 확신할 수 있으며(왜냐면 A에서 B로 가는 더 짧은 길이 있으려면 애초에 A에서 다음 방문할 가장 짧은 노드가 B가 아니라 다른 인접 노드였어야 했으므로), 완료 표시를 하는 것이 make sense하다.
이렇게 소스 노드(A)에서 가장 가까운 노드부터 하나씩 최단 거리를 구하는 것이 바로 Dijstra 알고리즘이다.
queue = [A]
while queue:
cur_node = queue.pop()
cur_node.complete = True
for neighbor_node in cur_node.neighbor_nodes:
next_visit_node, min_dist = None, float('inf')
# edge relaxation
if not neighbor_node.complete:
if cur_node.distance + graph_distance < neighbor_node.distance:
neighbor_node.distance = cur_node.distance + graph_distance
neighbor_node.prev_node = cur_node
if neighbor_node.distance < min_dist:
next_visit_node = neighbor_node
min_dist = neighbor_node.distance
# 현재 노드에서 가장 가까운 다음 노드 (힙으로 할 수도 있음)
queue.append(next_visit_node)
Kruskal
- 최소 신장 트리를 찾는 알고리즘
- 알고리즘 실행 순서
- 모든 엣지(edge)를 가중치를 기준으로 오름차순 정렬한다
- 정렬된 엣지를 하나씩 가져와 연결하고, cyclic한지 체크. acyclic한 경우만 선택 -> cyclic한지는 Union Find 이용
- N-1개의 엣지를 선택할때 까지 2를 반복
Kahn’s Algorithm
- 위상 정렬에서 가장 많이 쓰이는 알고리즘
- 원소들간의 우선순위가 있을 때, 우선순위를 고려하여 정렬
- ex. 미적분학 -> 물리학 -> 반도체 공학 이런식으로 반도체 공학을 듣기 위해 물리학을 먼저 들어야만 하고, 물리학을 듣기 위해 미적분학을 반드시 들어야 하는 상황
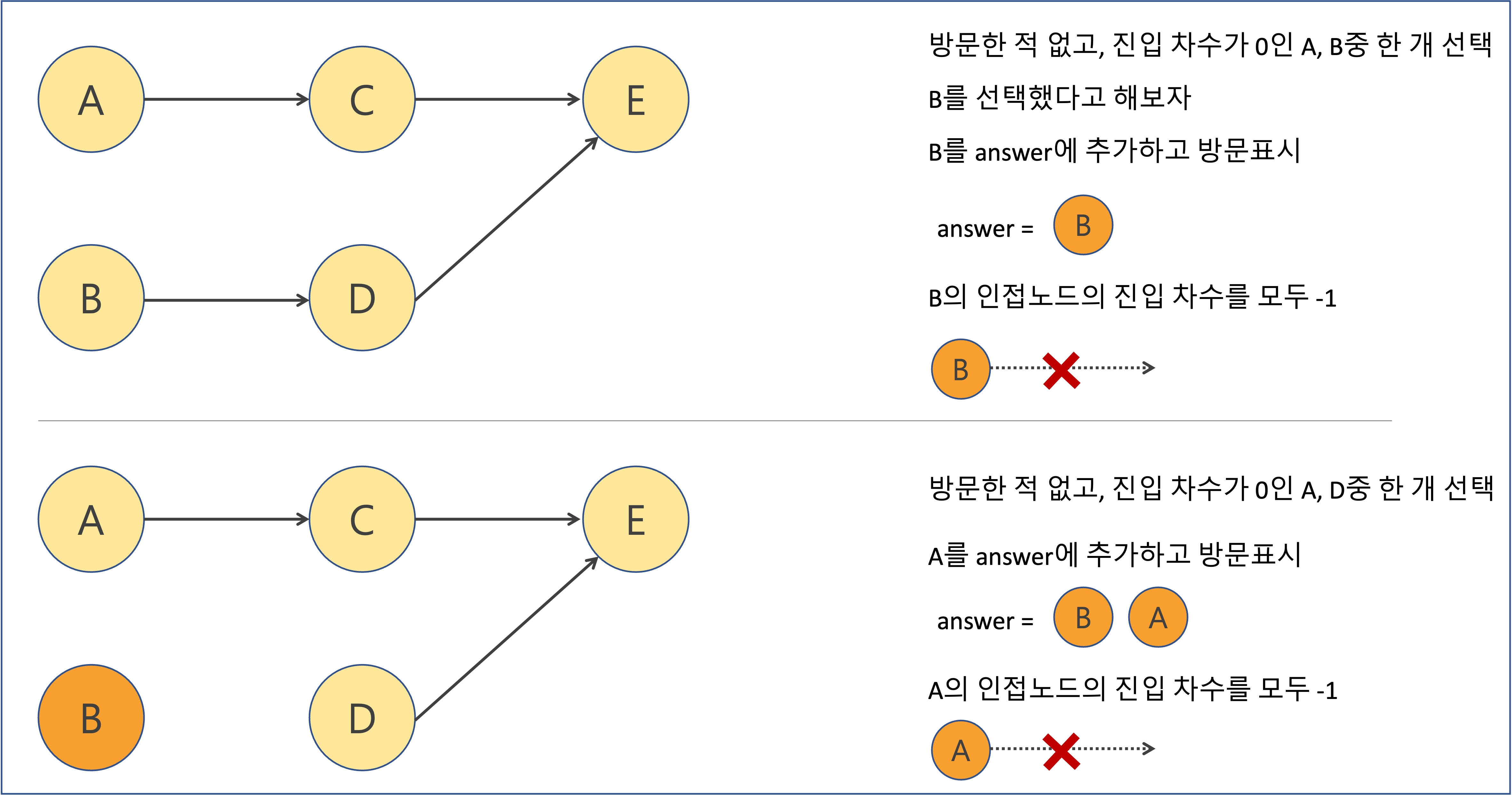
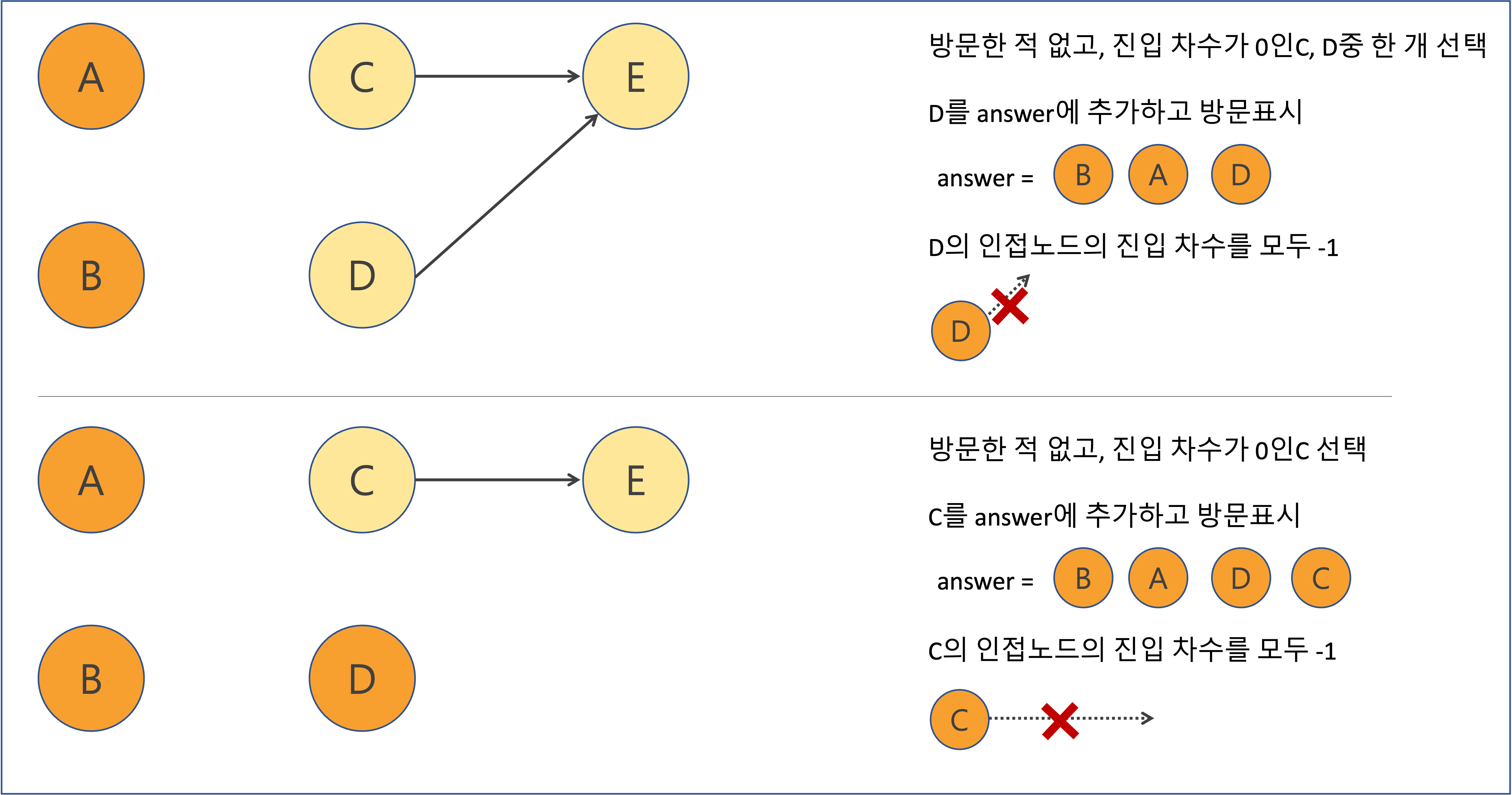
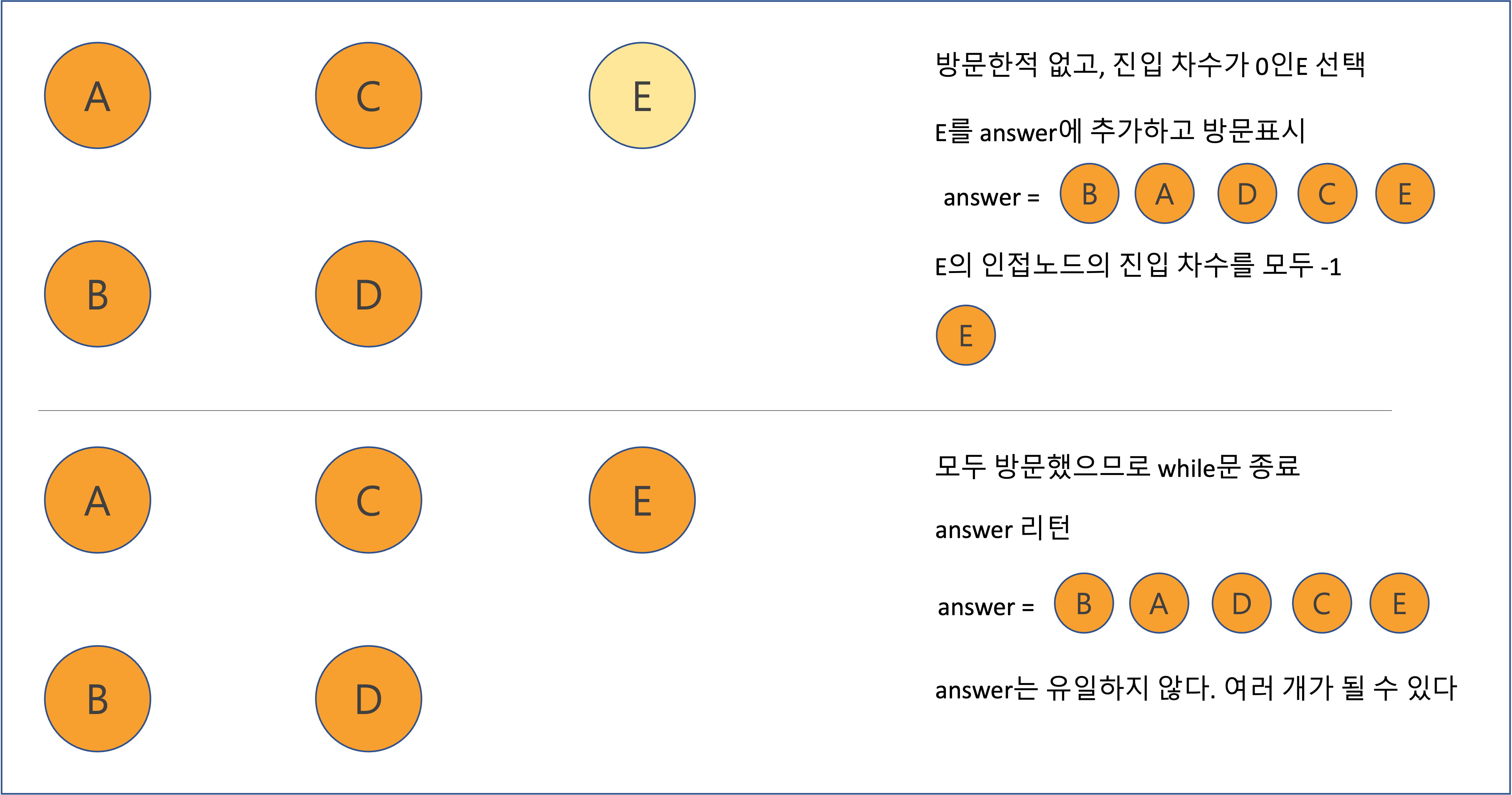
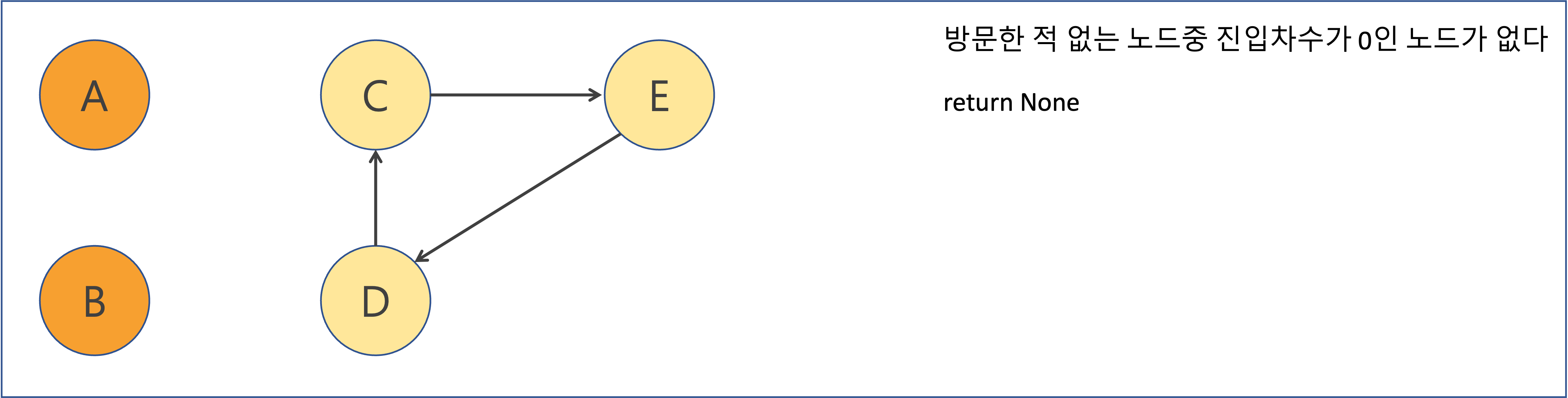
- 진입차수가 0이고 방문한 적이 없다면 해당 노드를 방문할 수 있다
- 어떤 노드의 진입차수가 0이라는 말은 그 노드보다 선행되는 노드가 없다는 말이며, 현재 시점에서 루트 노드라는 뜻이다
그림으로 Kahn’s Algorithm 과정을 한 번 살펴보자.
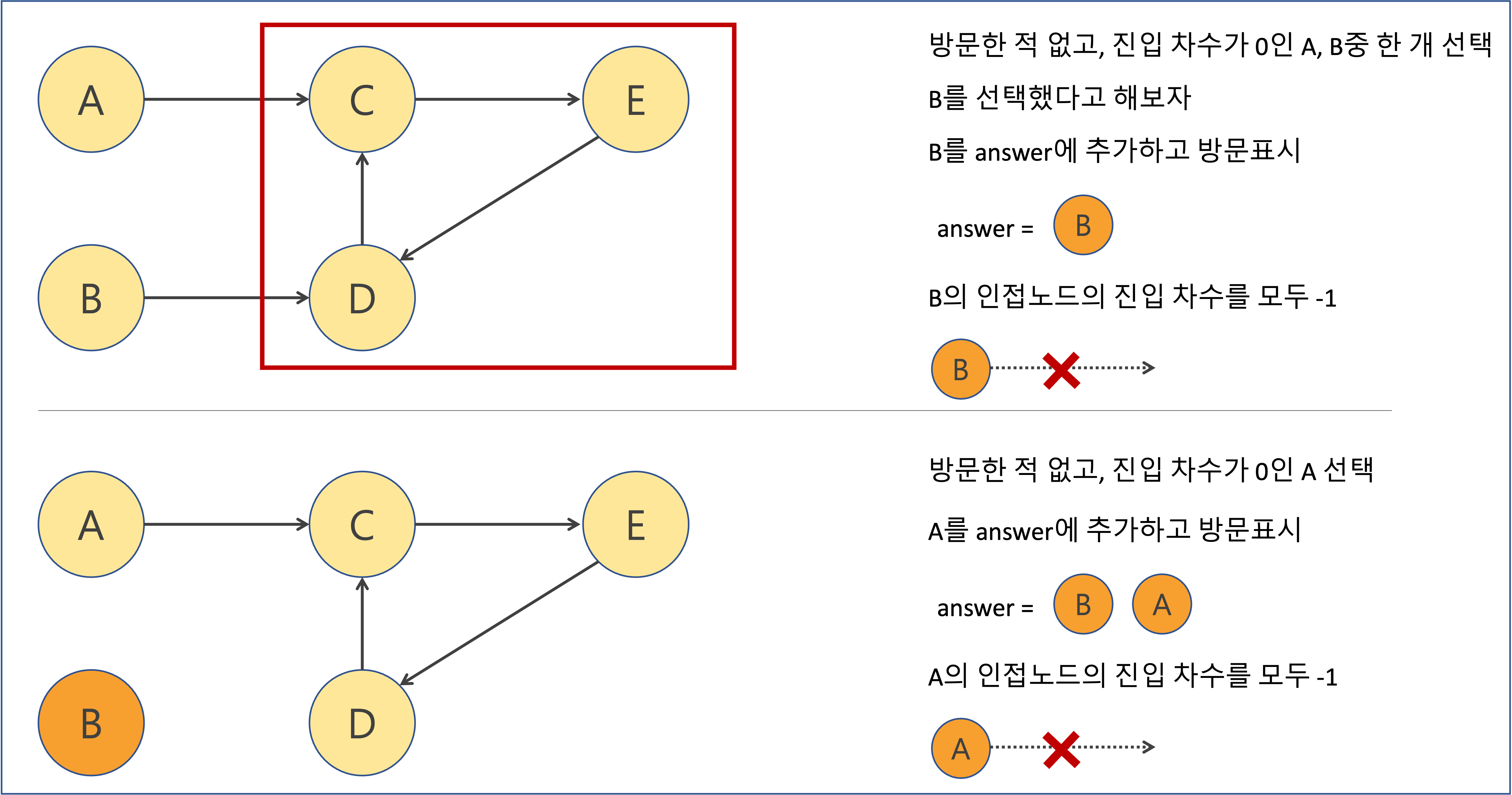
만약 노드간 cyclic이 있으면 그래프는 위상정렬할 수 없다.



































![[Data Structure] Graph (4): Dijkstra, Kruskal, Kahn's Algorithm](/images/data-structure_logo.png)
