![[Data Structure] Graph (1): 그래프](/images/data-structure_logo.png){kind=logo}
Table of Contents
Graph
그래프의 정의
- 노드(Node)와 노드를 연결하는 간선(Edge)으로 구성된 자료구조
- 노드간의 관계를 표현하는데 사용되는 자료구조
트리와 그래프의 차이
트리
- 트리는 그래프의 특별한 케이스
- 그래프의 정의 + 몇 가지 조건
- 그래프의 정의: 노드(Node)와 노드를 연결하는 간선(Edge)으로 구성된 자료구조
- 몇 가지 조건
- 노드 사이를 연결하는 간선은 모두 1개씩만 존재한다 (노드의 수가 V개 이면, 간선의 수는 V-1개)
- 루트 노드가 있다 (부모-자식이라는 계층적 관계가 있다, 부모 노드에서 자식 노드라는 방향이 있다)
- 비순환
- 위의 내용을 종합해 트리를 DAG(Directed Acyclic Graph)이라고도 한다
- 트리의 종류: 이진트리, 이진탐색트리, 힙트리, B-트리 등
- 트리 예시: 회사 조직도
그래프
- 트리에는 없는 그래프만의 특징
- 순환/비순환으로 구분된다
- 방향/무방향으로 구분된다
- 간선에 가중치가 있는 경우도 있다
- 노드를 잇는 간선이 2개 이상인 경우도 있다
- 그래프 예시: SNS, 지하철 노선, 지도
- 순환/비순환 + 방향/무방향 + 가중치/비가중치 그래프
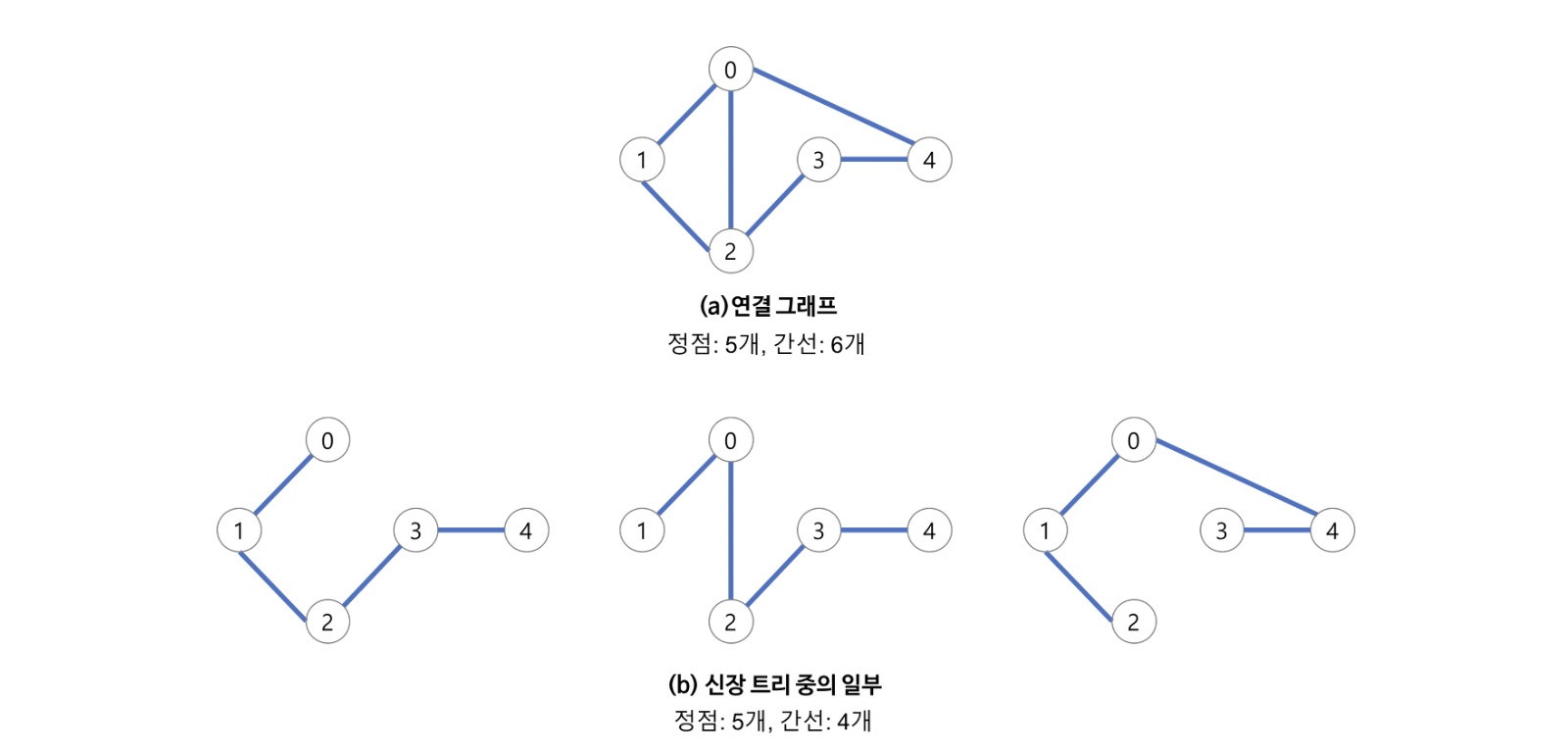
신장 트리(Spanning Tree)
- 신장 트리는 그냥 그래프에서 유래된 ‘트리’
- 그래프가 주어졌을 떄 V-1개의 간선만 남기고 다른 간선들은 제거한다
- 남은 V-1개의 간선으로 이루어진 그래프가 비순환하다면 트리가 된다 -> 이렇게 만들어진 트리를 ‘신장 트리’라고 한다
- 1개의 그래프에 1개 이상의 신장 트리가 만들어진다
- 가중치 그래프인 경우 남은 간선들의 가중치 합을 최소로 하는 신장 트리를 ‘최소 신장 트리’라고 한다
- 신장 트리의 예시: 통신 네트워크 구축
Graph와 관련한 문제 유형
그래프 탐색(모든 정점 방문)
- 그래프에서 사용하는 탐색 알고리즘
- DFS(Depth First Search)
- 깊이 우선 탐색
- 재귀함수 또는 반복문으로 구현
- BFS(Breadth First Search)
- 너비 우선 탐색
- 반복문으로 구현
- DFS(Depth First Search)
- 트리에서 사용하는 탐색 알고리즘
- Preorder, Inorder, Postorder, Level-order
그래프 최단 거리(두 정점간 가능한 모든 경로 찾기)
- 최단 경로에서 사용하는 알고리즘
- 그래프 탐색 알고리즘와 마찬가지로 DFS, BFS
- 시간 복잡도 낮추기 위해 백트래킹(Backtracking) 추가 가능
- (특별한 것 아니고 그냥 가지치기)
- (중간에 조건을 만족하지 않게 되면 탐색 중단)
- 가중치 있는 그래프의 최단 경로 알고리즘
- Dijkstra 알고리즘
- 음의 가중치 가지는 경우: Bellman-Ford 알고리즘
모든 정점에서 다른 모든 정점까지의 최단 경로
- 모든 정점들간의 경로중 최단 경로 찾는 알고리즘
- Floyd-Warshall 알고리즘 (DP와 연관)
그래프 분석
- Disjoint Set (or Union-FInd)
- Union-Find라고도 불리는 이유는 Disjoint Set 자료구조가 가지는 가장 중요한 메소드가 union과 find
- 용도
- 두 노드가 서로 연결되어 있는가
- Detect Cycle: 그래프가 순환 그래프인가
- 현재 선택된 엣지로 연결된 두 노드가, 하나의 집합이라면(서로 연결되어 있다면)
- 이 엣지를 선택하게 되면 그래프는 순환 그래프가 된다
- 구현 방법
- Quick Union
- Quick Find
최소 신장 트리
- 그래프에서 최소 신장 트리 찾는 알고리즘
- Kruskal 알고리즘 (Union-Find와 관련)