Union-Find

The primary use of Union-Find is to address the connectivity between the components of a network.

Key points of Union-Find

find: function finds the root node of a given vertex.
union: function unions two vertices and makes their root nodes the same.

Use Case of Union-Find

Determine Connection
Detect Cycle

Implementation of Union-Find

Quick Find

self.root의 인덱스는 자기 자신, 값은 루트 노드를 가리킴
self.root의 값 자체가 인덱스 노드의 루트 노드이기 때문에 find는 O(1)
x와 y를 union하기 위해 x와 같은 루트 노드를 가지는 모든 노드의 루트 노드를 y의 루트 노드로 변경 -> 항상 O(N)
find는 O(1). union은 O(N)

# Quick Find
class UnionFind:
    def __init__(self, size):
        self.root = [i for i in range(size)]
    
    def find(self, x):
        return self.root[x]
    
    def union(self, x, y):
        if self.root[x] != self.root[y]:
            root_x = self.find(x)
            root_y = self.find(y)
            for i in range(len(self.root)):
                if self.root[i] == root_x:
                    self.root[i] = root_y
    
    def connected(self, x, y):
        if self.find(x) == self.find(y):
            return True
        return False

uf = UnionFind(9)

edges = [(0, 1), (0, 2), (1, 3), (4, 8), (5, 6), (5, 7)]

for edge in edges:
    uf.union(*edge)

print(uf.connected(0, 3))
print(uf.connected(1, 5))
print(uf.connected(7, 8))

Quick Union

self.parent의 인덱스는 자기 자신, 값은 부모 노드를 가리킴
self.parent의 배열에서 계속 부모 노드를 타고 올라가면서 루트 노드가 나올 때 까지 반복 -> find는 O(N)
x의 루트 노드의 부모 노드를 y의 루트 노드로 변경 -> union도 O(N)
find와 union 모두 O(N)이기 때문에 Quick Union이 시간 측면에서 성능이 낮아보이지만 union은 최악의 경우만 O(N)이지 Quick Find처럼 항상 O(N)은 아니다. 두 메소드 모두 정확히는 루트 노드를 찾는 과정만 필요로 하므로 정확히는 O(H)이다.
union, find -> O(H). (H는 해당 노드에서 루트 노드까지의 높이)

# Quick Union
class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]
    
    def find(self, x):
        while x != self.parent[x]:
            x = self.parent[x]
        return x
    
    def union(self, x, y):
        if self.parent[x] != self.parent[y]:
            root_x = self.find(x)
            root_y = self.find(y)
            self.parent[root_x] = root_y
    
    def connected(self, x, y):
        if self.find(x) == self.find(y):
            return True
        return False

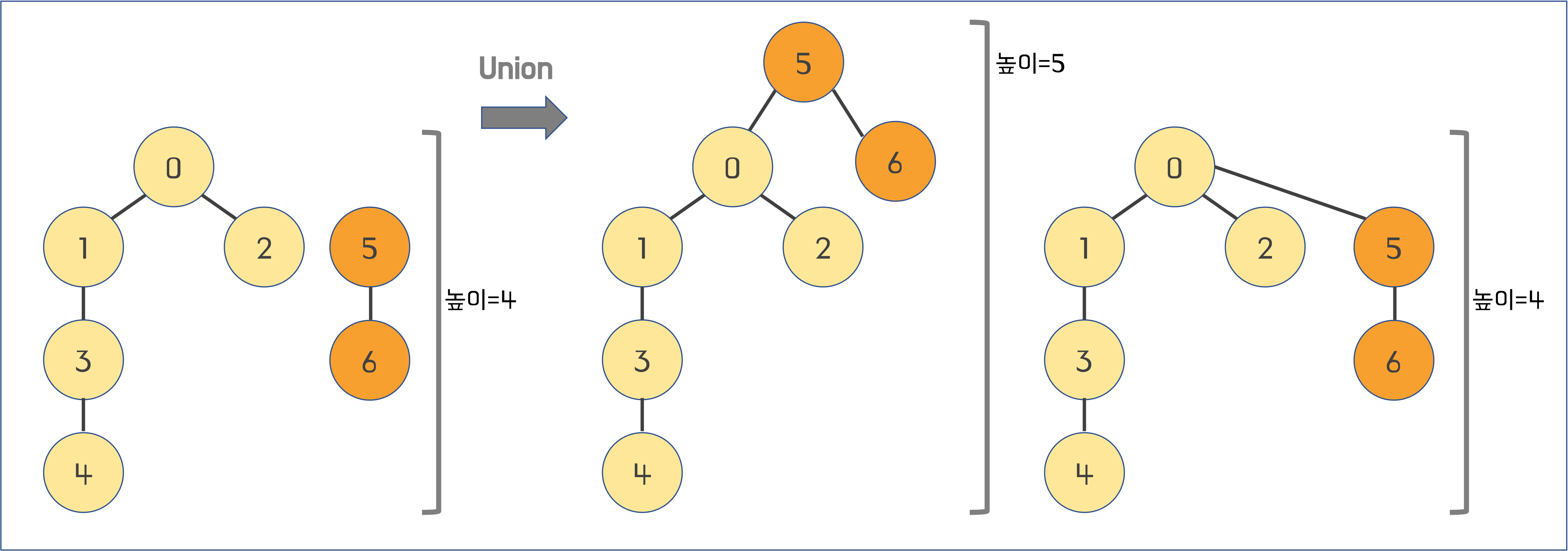
Union by Rank

rank: 각 노드의 높이
union하고자 하는 두 트리의 루트 노드의 rank를 비교
rank가 높은 트리의 루트 노드가 union된 결과의 루트 노드가 되도록 하자 -> 최종 결과 트리의 높이가 유지될 수 있음
두 트리의 높이가 같으면 임의로 하나를 기준 루트 노드로 잡는다 -> 하지만 rank가 1증가 할 수 밖에 없음
Quick-Union의 union 메서드를 개선한 방법
Quick Union에서 O(H)가 O(N)이 아닌 O(logN)으로 되도록 함
union된 결과가 일자로 길어지는 상황을 피할 수 있음

# Union by rank
class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]
        self.rank = [1] * size
    
    def find(self, x):
        while x != self.parent[x]:
            x = self.parent[x]
        return x
    
    def union(self, x, y):
        if self.parent[x] != self.parent[y]:
            root_x = self.find(x)
            root_y = self.find(y)
            if self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            elif self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            else:
                self.parent[root_x] = root_y
                self.rank[root_y] += 1
            
    
    def connected(self, x, y):
        if self.find(x) == self.find(y):
            return True
        return False

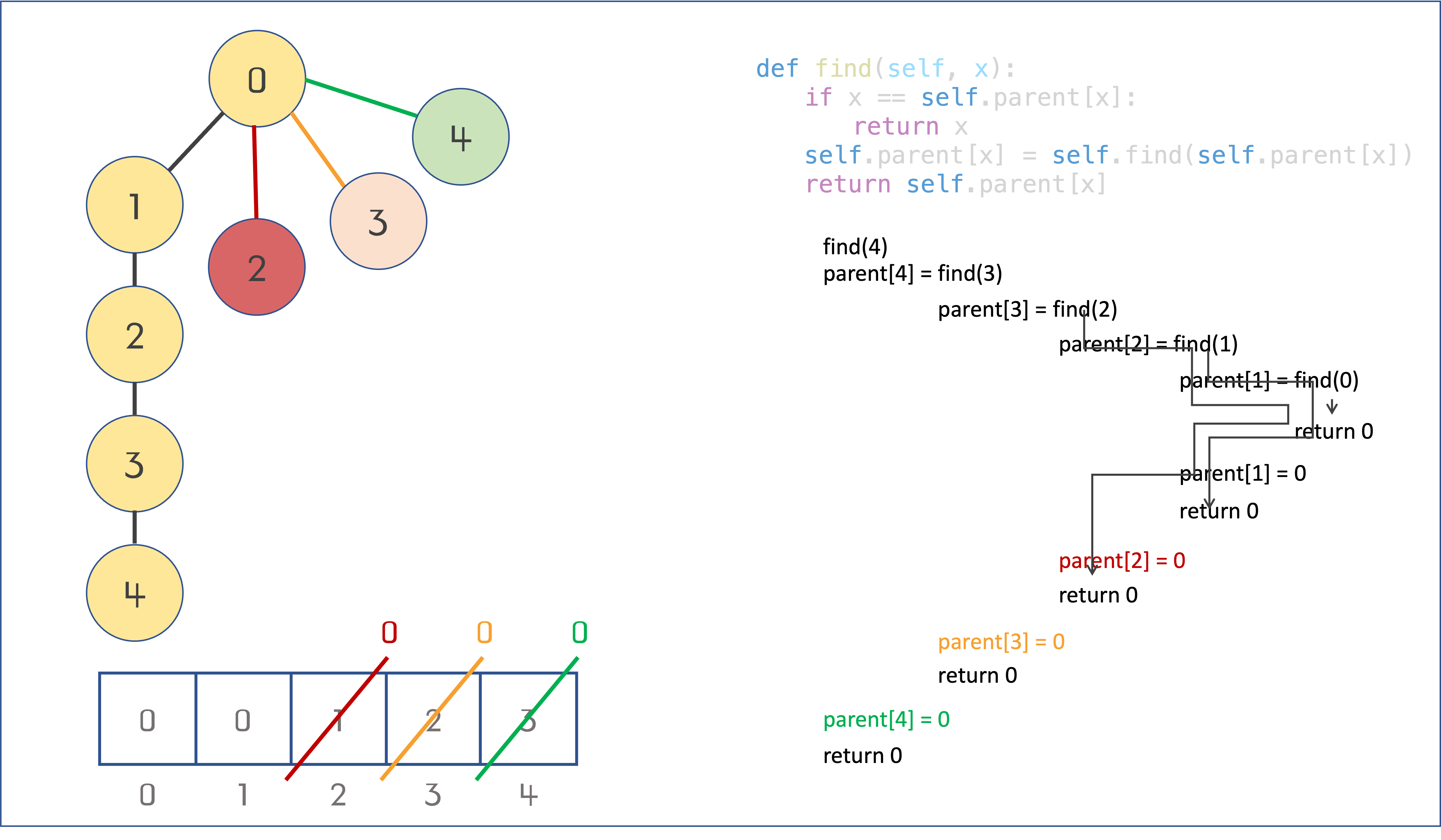
Path Compression

기존 Quick Union에서 find는 루트 노드를 찾기 위해 parent를 계속 traverse함
If we search the root node of the same element again, we repeat the same operations. Is there any way to optimize this process?
After finding the root node, we can update the parent node of all traversed elements to their root node. When we search for the root node of the same element again, we only need to traverse two elements to find its root node, which is highly efficient. So, how could we efficiently update the parent nodes of all traversed elements to the root node? The answer is to use “recursion”. This optimization is called “path compression”, which optimizes the find function.
대상 노드의 루트 노드를 찾는 과정에서 거쳐가는 모든 노드의 루트 노드를 찾아 저장한다

# Path compression
class UnionFind:
    def __init__(self, size):
        self.parent = [i for i in range(size)]
        self.rank = [1] * size
    
    # Path Compression
    def find(self, x):
        if x == self.parent[x]:
            return x
        self.parent[x] = self.find(self.parent[x])
        return self.parent[x]
    
    def union(self, x, y):
        if self.parent[x] != self.parent[y]:
            root_x = self.find(x)
            root_y = self.find(y)
            if self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            elif self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            else:
                self.parent[root_x] = root_y
                self.rank[root_y] += 1
            
    
    def connected(self, x, y):
        if self.find(x) == self.find(y):
            return True
        return False