Table of Contents
기술 통계
- 수집한 데이터의 경향이나 성질을 수치나 표, 그래프 등으로 표현하는 방법
- 기술 통계에서 크게 관심 있는 부분은 첫 번째 Central Tendency(Mean, Median, Mode(최빈값)), 두 번째 Dispersion(Range, Standard deviation, Variance) 그리고 세 번째로 Distribution 이다
대표값(Central Tendency)
- 데이터 전체의 특징을 하나의 값으로 표현하는 방법
- 대표적인 대표값으로는 평균값, 중앙값, 최빈값이 있다
- 대표값을 알더라도 분포를 모르면 알 수 있는 내용은 많지 않다
평균값(mean)
- 평편하고 균일하게 만든 값
- 통계에서 가장 많이 사용하는 평균 계산법은 산술평균 (x1 + x2 + … + xn / n)
중앙값(median)
- 데이터를 크기순으로 나열했을 때 순서상 가운데 있는 값
- 평균값과 중앙값을 알면 대략적인 분포를 예측할 수 있다
- 데이터의 개수가 홀수면 중앙값은 정확히 가운데 값, 짝수면 중앙에 있는 두 값의 평균
- 데이터에 아웃라이어 값이 있을 때는 평균값보다 중앙값이 데이터를 더 잘 대표한다
대표값으로 예측하는 데이터 분포
- 평균값 = 중앙값: 분포가 좌우대칭이다
- 평균값 < 중앙값: 분포가 오른쪽으로 치우쳐있다
- 평균값 > 중앙값: 분포가 왼쪽으로 치우쳐있다
Dispersion
- 평균값을 기준으로 데이터의 흩어진 정도는 표준편차로 알 수 있다
- 평균에서 각 데이터가 흩어진 정도는 편차(deviation)로 나타낼 수 있다 (편차 = x_i - 평균)
분산
- 편차는 평균을 구해보면 항상 0이다. 그래서 각 편차를 제곱해서 평균을 구하면 그 값이 곧 분산(variance)이다
- 분산값이 평균에서 흩어진 정도를 나타내는 하나의 값이 된다
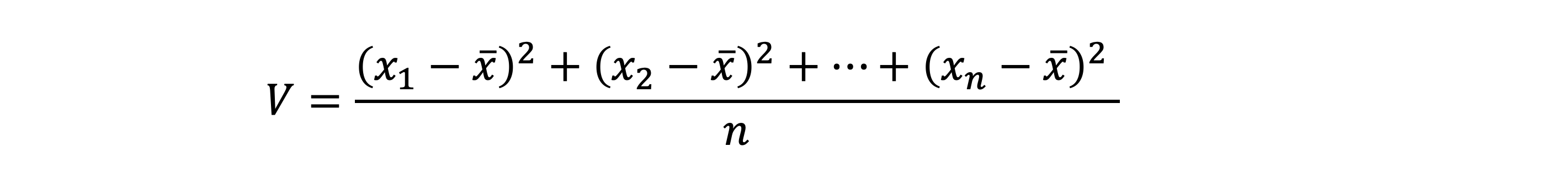
- 분산 식을 조금 더 간단하게 표현하면 아래와 같다
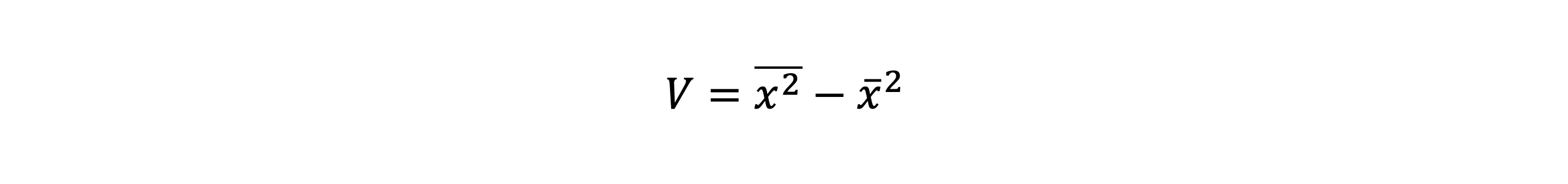
표준편차
- 분산은 단위가 원래의 제곱이 된다는 문제가 있다
- 그래서 분산에 제곱근을 한 값을 표준편차(standard deviation)이라 한다
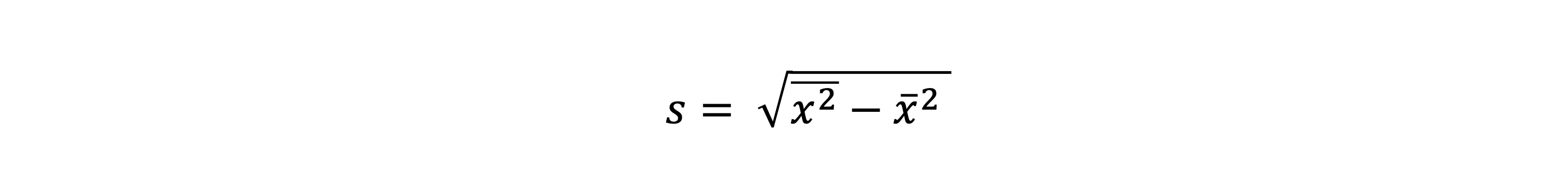
Distribution
도수분포표와 히스토그램
- 데이터의 분포를 확인하는 대표적인 기술통계는 도수분포표와 히스토그램이다
- 데이터가 흩어진 정도를 파악
- 데이터를 적당한 구간으로 계급화해 각 계급에 속하는 데이터 수의 분포를 파악할 수 있다
- 스터지스 공식에 따르면, 데이터의 수가 2n 개일 때, 적절할 계급의 개수는 n+1 개이다
- 도수분포표를 그래프로 나타낸 것을 히스토그램이라고 한다
도수분포표
- 계급: 각 구간
- 계급값: 각 계급의 중간값
- 도수: 각 계급에 포함된 데이터의 수
data = pd.Series([random.randint(0, 100) for _ in range(1000)])
data

freq_data = pd.cut(x=data,
bins=[-1, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
freq_data

df = freq_data.value_counts().to_frame()
df.index.name = "계급"
df.sort_index(inplace=True)
df.columns = ['도수']
class_values = []
for i in range(len(df)):
class_values.append(df.index[i].mid)
df['계급값'] = class_values
df

히스토그램
fig, ax = plt.subplots(figsize=(12, 5))
ax.bar([str(i) for i in df.index.values], df['도수'])

상대도수와 누적 상대도수
tot = df['도수'].sum()
relative_freq_values = []
for i in range(len(df)):
relative_freq_values.append(df.iloc[i, 0]/tot)
df['상대도수'] = relative_freq_values
df['누적상대도수'] = df['상대도수'].cumsum()

4분위수와 상자수염도
4분위수
- 중앙값을 기준으로 데이터의 흩어진 정도를 나타내는 값
- Q1, Q2, Q3
- Q1: 데이터를 크기순으로 나열했을 때 순서상 25%에 해당하는 값
- Q2: 순서상 50%에 해당하는 값 (중앙값)
- Q3: 순서상 75%에 해당하는 값
data.describe()

상자수염도
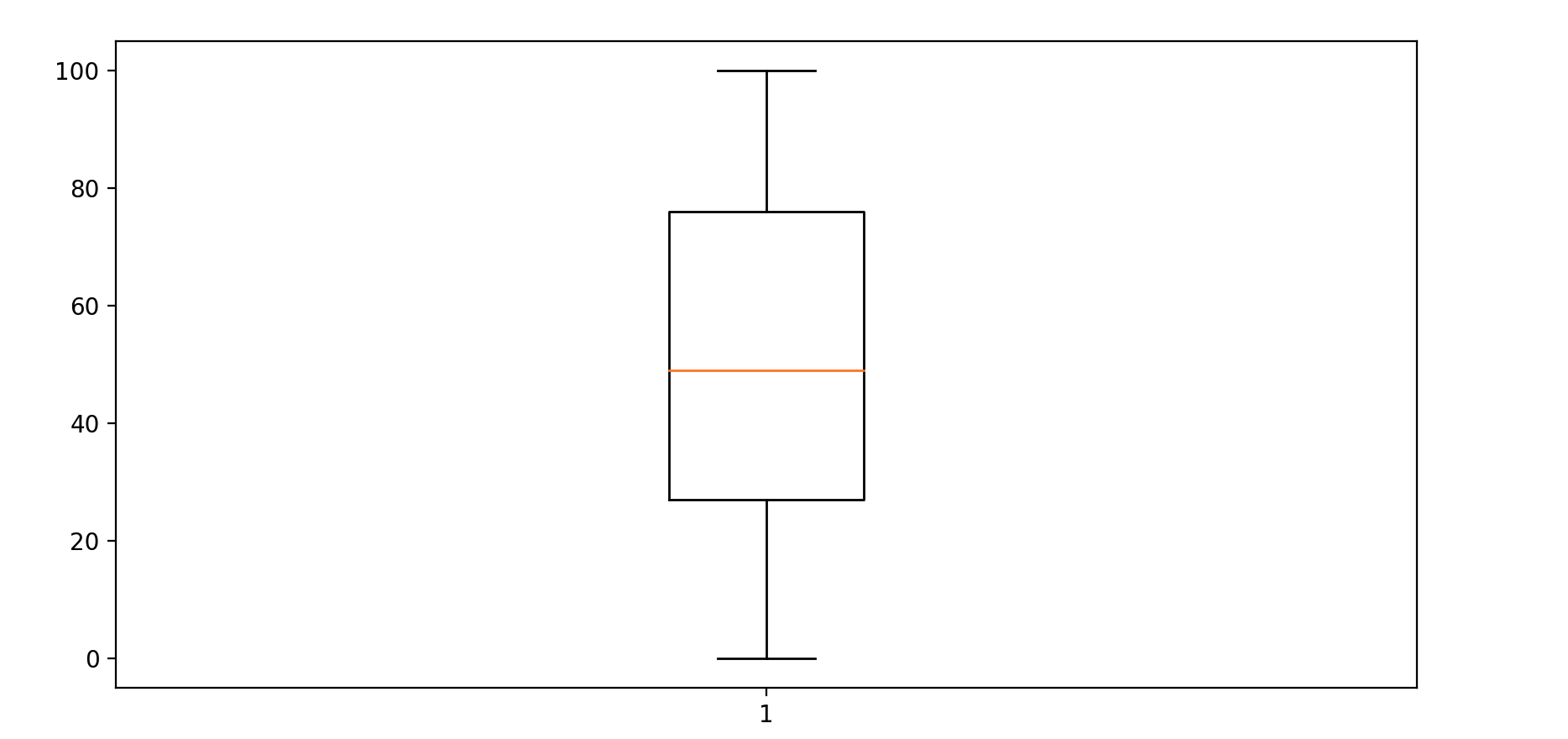
상관관계와 산포도
- 상관관계는 2변량 데이터의 변량간 경향성을 나타낸다
- 한쪽이 증가할 때 다른 쪽도 증가하는 경향을 양의 상관관계에 있다고 한다
- 공분산은 상관관계의 세기를 수치화 하는 방법이다
- 공분산만으로는 A 데이터셋의 상관관계와 B 데이터셋의 상관관계의 정도를 비교할 수 없다 (공분산은 단위가 커지면 같이 커진다)
- 상관계수를 이용하면 여러 데이터셋간의 상관관계를 비교해 어떤 데이터셋이 더 큰 상관관계를 있는지 대소관계를 비교할 수 있다
공분산을 구하는 방법
- (x1, y1) 데이터의 편차곱
(x1 - x의 평균) X (y1 - y의 평균)의 평균이 공분산 값이다
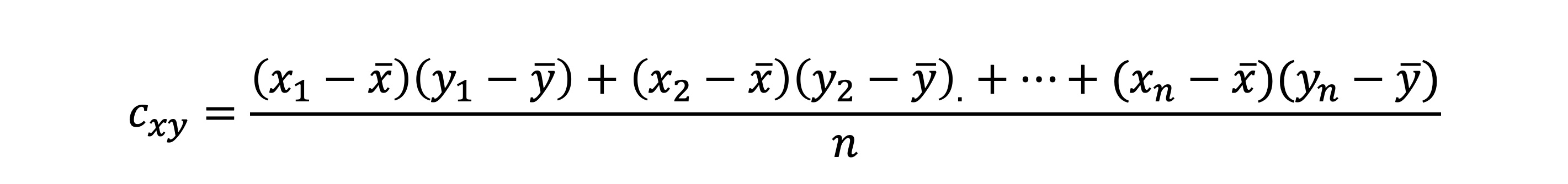
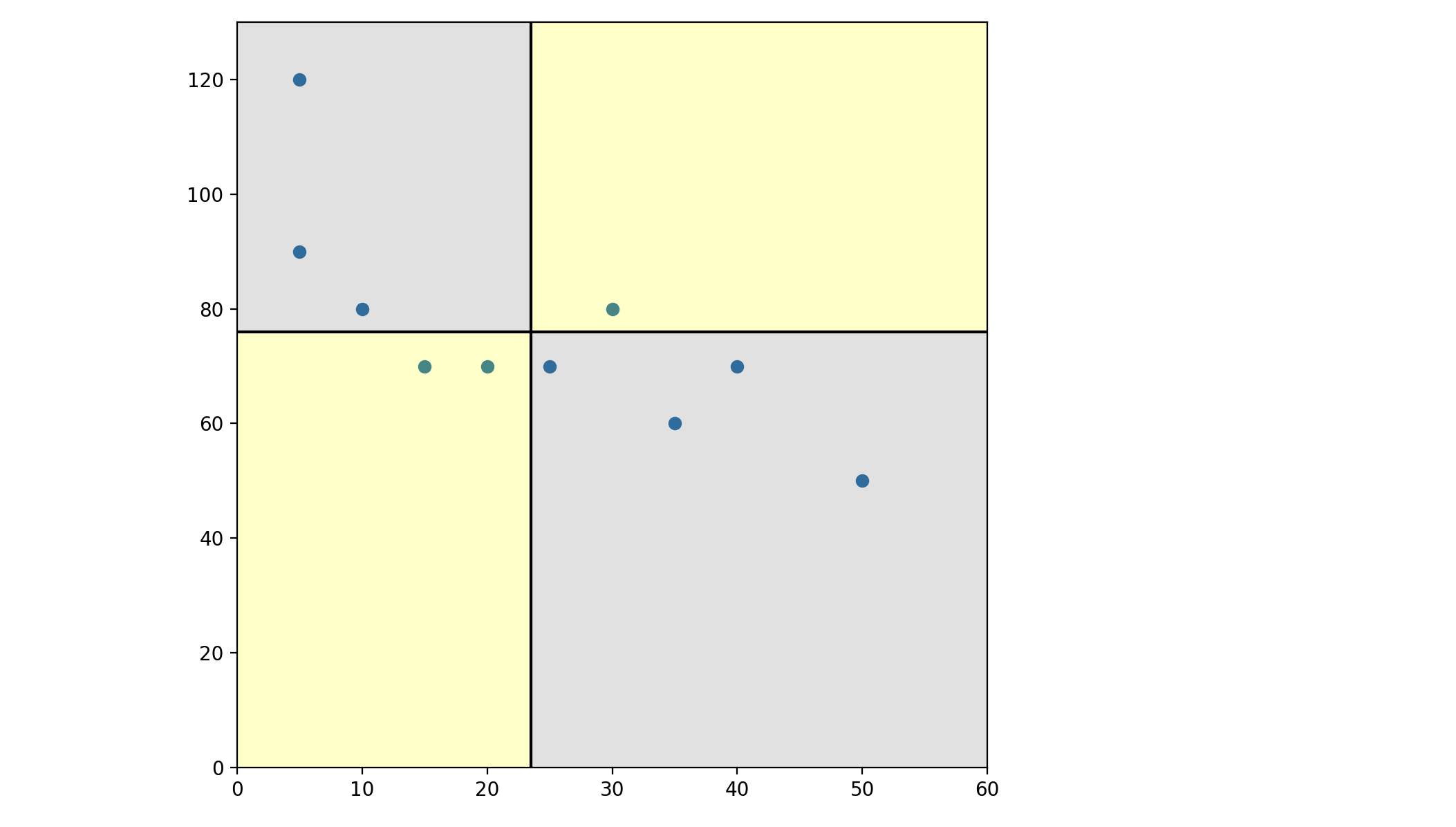
- 노란색 영역과 회색 영역을 표시해둔 이유는, 노란색 영역은 편차곱이 양수, 회색 영역은 편차곱이 음수이다
- 그래서 노란색 영역에 데이터가 많이 분포하면 공분산값이 양수가 되고, 회색 영역에 많이 분포하면 공분산값이 음이 된다
상관계수 구하는 방법
- 상관계수는 공분산을 각 변량의 표준편차로 나누면 된다
- 상관계수는 단위가 바뀌어도 영향을 받지 않는다 (ex. 원에서 만원으로 바꿔도 상관 없다)
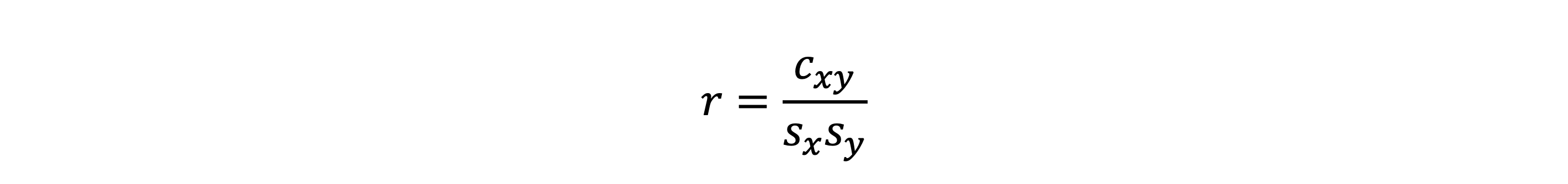



































![Statistics and Probability Series [Part2]: 기술통계](/images/probability_logo.jpeg)
