Table of Contents
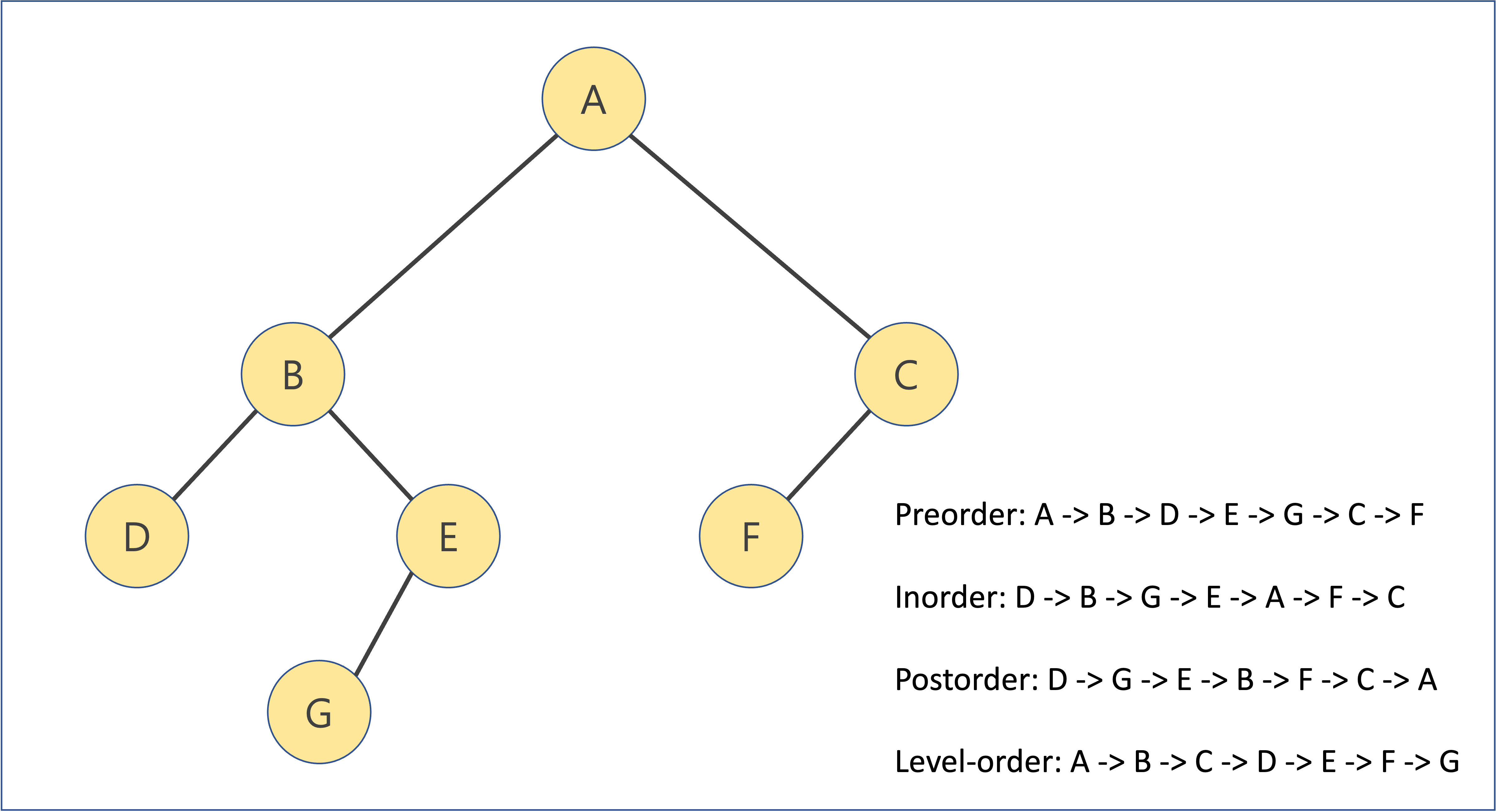
이진 트리를 순회하는 방법은 크게 Preorder, Inorder, Postorder, Level-order가 있다.
- Preorder: 자신의 노드 방문 -> 왼쪽 자식 노드 방문 -> 오른쪽 자식 노드 방문 (Graph의 DFS와 결과가 같다)
- Inorder: 왼쪽 자식 노드 방문 -> 자신의 노드 방문 -> 오른쪽 자식 노드 방문
- Postorder: 왼쪽 자식 노드 방문 -> 오른쪽 자식 노드 방문 -> 자신의 노드 방문
- Level-order: 루트 노드 방문 -> 깊이가 1인 노드 방문 -> 깊이가 2인 노드 방문 .. -> 리프 노드 방문
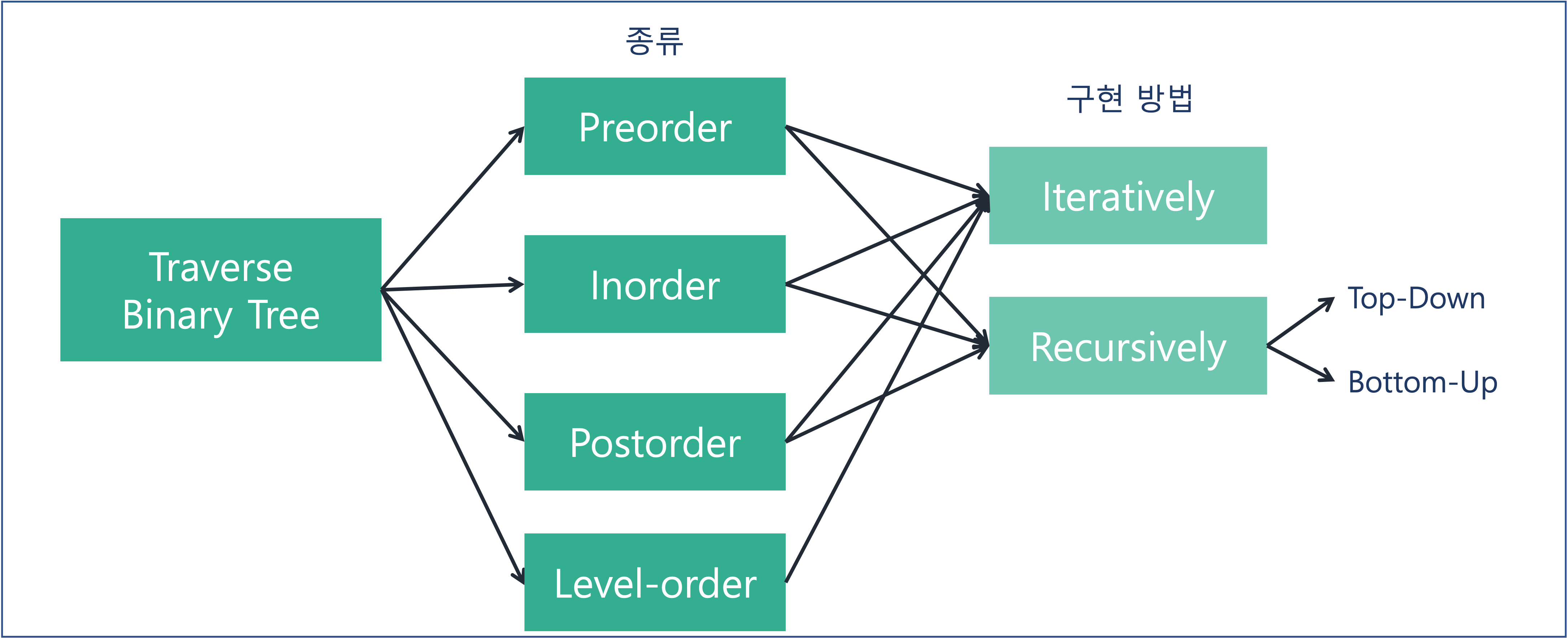
이진 트리 순회를 구현하는 방법
Iteration
Preorder
첫 번째 방법
현재 꺼낸 노드를 정답에 추가
자식 노드 여부에 따라 스택(to_visit)에 추가
def preorder(root):
visited = []
to_visit = [root]
while to_visit:
now_node = to_visit.pop()
visited.append(now_node.val)
if now_node.right:
to_visit.append(now_node.right)
if now_node.left:
to_visit.append(now_node.left)
return visited
두 번째 방법
매번 본인 노드를 방문할 차례가 아니라면 오른쪽 자식 노드, 본인, 왼쪽 자식 노드를 스택에 추가
본인 노드를 추가할 때는 (본인 노드가 다시 스택에서 꺼내질때는 방문할 차례가 되었기 때문에) True로 표시
def preorder(root):
res, stack = [], [(root, False)]
while stack:
node, visited = stack.pop()
if node:
if visited:
res.append(node.val)
else:
stack.append((node.right, False))
stack.append((node.left, False))
stack.append((node, True))
return res
Inorder
첫 번째 방법
매번 본인 노드를 방문할 차례가 아니라면 오른쪽 자식 노드, 본인, 왼쪽 자식 노드를 스택에 추가
본인 노드를 추가할 때는 (본인 노드가 다시 스택에서 꺼내질때는 왼쪽 자식 노드를 방문을 마친 후기 때문에) True로 표시
def inorder(root):
res, stack = [], [(root, False)]
while stack:
node, visited = stack.pop()
if node:
if visited:
res.append(node.val)
else:
stack.append((node.right, False))
stack.append((node, True))
stack.append((node.left, False))
return res
두 번째 방법
왼쪽 자식 노드가 있을 때마다 최대한 깊숙히 들어간 다음 왼쪽 자식 노드가 없으면 자기 자신의 노드를 정답에 추가(방문 표시)하고,
오른쪽 자식 노드가 있으면 오른쪽 자식 노드로 접근. 더이상 방문할 노드가 없으면 반복문 종료
def inorder(root):
res, stack = [], []
# this following "while True" block keeps running until "return"
while True:
# goes all the way to left end's None, append every step onto "stack"
while root:
stack.append(root)
root = root.left
# if stack has nothing left, then return result
if not stack:
return res
# take the last step out, append its value to result
node = stack.pop()
res.append(node.val)
# moves to right before going all the way to left end's None again
root = node.right
Postorder
첫 번째 방법
매번 본인 노드를 방문할 차례가 아니라면 오른쪽 자식 노드, 본인, 왼쪽 자식 노드를 스택에 추가
본인 노드를 추가할 때는 (본인 노드가 다시 스택에서 꺼내질때는 왼쪽/오른쪽 자식 노드를 방문을 마친 후기 때문에) True로 표시
def postorder(root):
res, stack = [], [(root, False)]
while stack:
node, visited = stack.pop()
if node:
if visited:
res.append(node.val)
else:
stack.append((node, True))
stack.append((node.right, False))
stack.append((node.left, False))
return res
Level-order
순서는 문맥상 Preorder와 비슷하다
하지만 Preorder는 노드를 스택에 쌓아서 순회하기 때문에 자신의 오른쪽 노드를 방문하기 전에 계속 왼쪽으로 깊이 들어간다
Level-order는 큐에 쌓아서 순회하기 때문에 자신의 할 일을 다하고 자식 노드에 넘겨준다
from collections import deque
def level_order_traverse(root):
res = []
queue = deque([root])
while queue:
cur_node = queue.popleft()
if cur_node:
res.append(cur_node.val)
queue.append(cur_node.left)
queue.append(cur_node.right)
return res
그래프를 직접 만들어 실행해보면 결과는 다음과 같다.
from collections import deque
class Node:
def __init__(self, val, left=None, right=None) -> None:
self.val = val
self.left = left
self.right = right
g_node = Node("G")
f_node = Node("F")
e_node = Node("E", g_node)
d_node = Node("D")
c_node = Node("C", f_node)
b_node = Node("B", d_node, e_node)
a_node = Node("A", b_node, c_node)
root_node = a_node
print(level_order_traverse(root_node))
--------------------------------------------------
['A', 'B', 'C', 'D', 'E', 'F', 'G']
Recursion
트리 순회를 Recursion으로 구현할 때는 크게 Top-Down approach와 Bottom-Up approach가 있습니다.
여기서 Top-Down, Bottom-Up은 DP에서도 사용하는 용어인데 값의 흐름을 얘기할 뿐, 같은 의미는 아닙니다.
(여기서 값은 숫자, 문자열, 리스트 등이 될 수 있습니다.)
Top-Down은 부모 노드를 처리하는 함수가 자신이 가지고 있는 값을 자식 노드를 처리하는 함수의 인자로 전달하는 접근법입니다.
def f(node, val):
if val == 0:
return
else:
f(node.left, val+1)
f(node.right, val-1)
Bottom-Up은 return문으로 계속 자식 노드를 처리하는 함수를 호출해 자식 노드를 처리하는 함수가 리턴하는 값을 계속 누적하는 접근법입니다.
def f(node):
return f(node.left) + f(node.right) + [node.val]
Preorder
# Bottom-Up
def preorder(root):
return [root.val] + preorder(root.left) + preorder(root.right) if root else []
# Top-Down
def preorder(root):
res = []
helper(root, res)
return res
def helper(root, res):
if root:
res.append(root.val)
helper(root.left, res)
helper(root.right, res)
Inorder
# Bottom-Up
def inorder(root):
return inorder(root.left) + [root.val] + inorder(root.right) if root else []
# Top-Down
def inorder(root):
res = []
helper(root, res)
return res
def helper(root, res):
if root:
helper(root.left, res)
res.append(root.val)
helper(root.right, res)
Postorder
# Bottom-Up
def postorder(root):
return postorder(root.left) + postorder(root.right) + [root.val] if root else []
# Top-Down
def postorder(root):
res = []
helper(root, res)
return res
def helper(root, res):
if root:
helper(root.left, res)
helper(root.right, res)
res.append(root.val)



































![[Data Structure] Binary tree (2): 이진 트리 순회](/images/data-structure_logo.png)
